
「途中計算、書くの面倒くさい」「途中計算を書けって言われるけど、どう書いたらいいかわからない」
そんな経験ないでしょうか?
途中計算って、数学が得意な人にとっては当たり前のように書けます。でも、そうでない人からすると「書いて何の意味があるの?」「何を書けばいいの?」と感じることが多いんです。明確なルールがあまりないので、わかりづらいんですよね。
ぼくは個別指導の校舎長を2年ほどしていました。そのときに厄介だなと思ったのが、数学が得意な人から見ると「途中計算を書かない=さぼっている」と見えてしまうこと。よく講師の大学生から、相談されました。
でも実際には、さぼっているわけではありません。途中計算を書く意義が分からなかったり、具体的な書き方を知らなかったりすれば、「書こう」という気持ちにならないのも当然なんです。
ただし、途中計算にはきちんと意味があり、書き方にもコツがあります。この記事では、塾講師時代に生徒に伝えていた内容をもとに、そのポイントをまとめてみます。
途中計算を書く意味
- 計算ミスが減る
頭の中だけで計算しようとすると、一時的に計算結果を覚えなければいけません。そうすると、ミスの元になってしまいます。 - 自分の弱点が見える
どこで間違えたかが分かるので、復習の効率が上がります。 - 計算ミスをみつけやすくなる
テスト当日の見直しのときに、間違いに気づきやすくなります。 - 加点対象になる
入試やテストでは、答えが合っていなくても式を書いていれば部分点がもらえることがあります。

途中計算を書いて勉強した方が、勉強する時間は短くて済みます。
おすすめの書き方
書き方に絶対のルールはありませんが、ぼくは次の2つのルールが基本です。
ここをスタートにして、演習を重ねて、自分なりに省略しても問題ないところを省略していってました。
それぞれ、どういうことか、OK例と、NG例を挙げながら見ていきます。
縦にそろえてつなげる
イコールをそろえて、上から下に処理していきます。たぶん、これは中学校で数学を習い始めたら、一番最初に言われると思います。こう書くと、式の区切りがよくわかります。たぶん、数学が得意な人はだいたいこう書いてるはず。
横にずっと書き続ける人がときどきいますが、式の区切りがわかりづらくなるのでやめたほうがいいです。
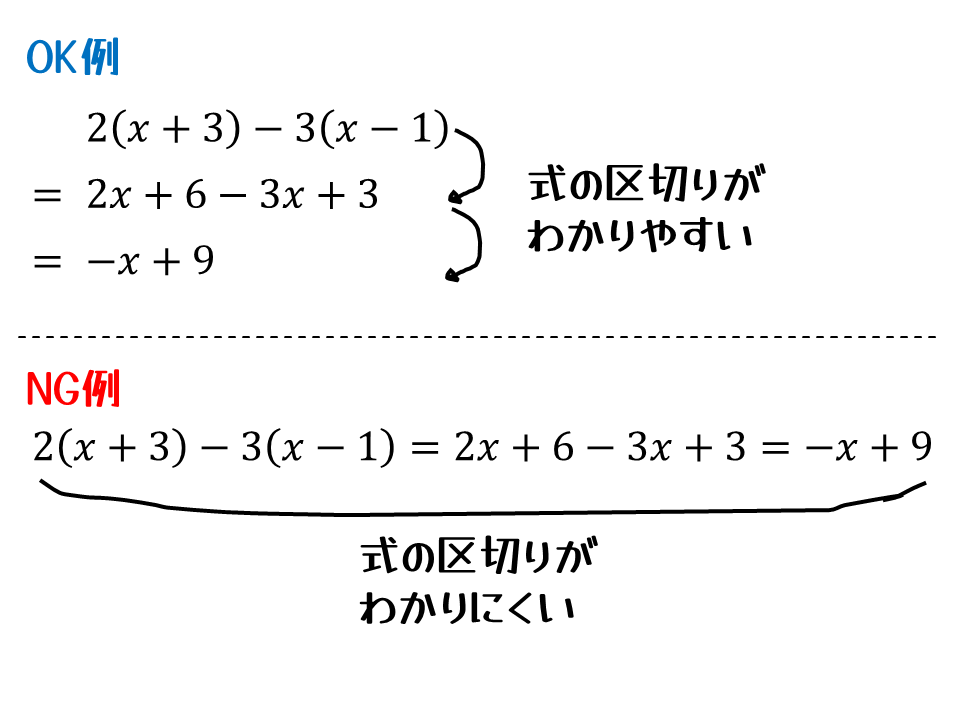
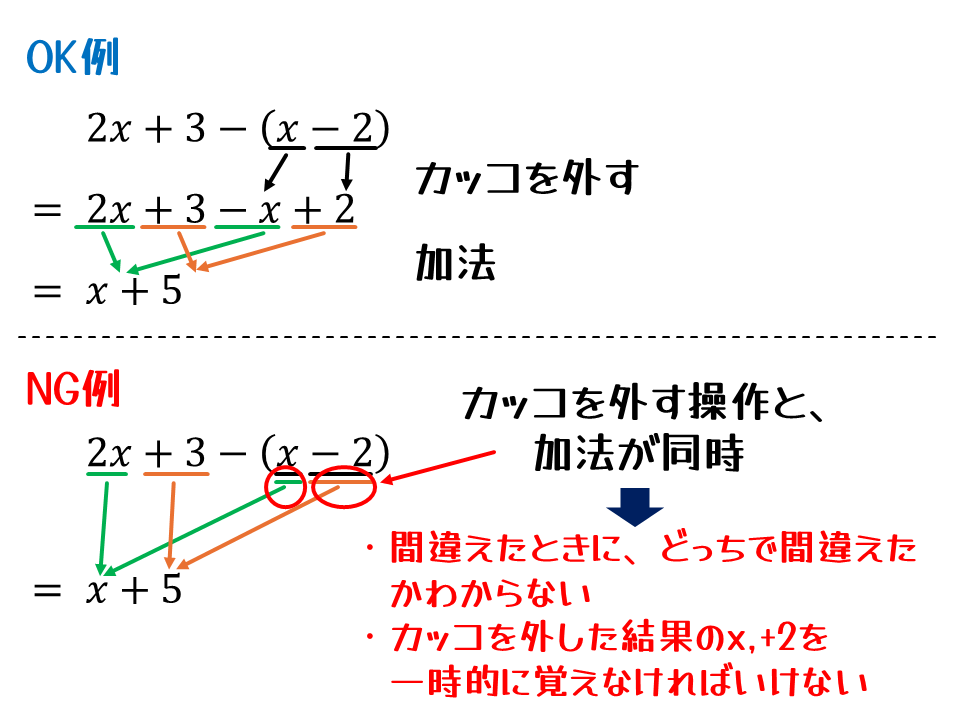
1つの項に操作は1回だけ
操作する項の数はいくつでもいいですが、1つの項に対しての操作を1回にします。こうすると、間違えたときに、どの操作で間違えたのかがわかりやすくなります。
逆に、式と式の間で、1つの項にいくつも操作をしてしまうと、どこで間違えたのかがわかりづらくなります。また、操作した結果を、一時的に覚えておかなければならないので、ミスしやすくなります。
NG例で書いた答案が間違っているわけではないですが、効率的に点で考えるとやめたほうがいいと思います。
中1の分野別で具体的に
中1の計算がメインになる分野で、具体例を見ていきます。塾で説明しているときは、こういう説明をしてました。
正負の数
この範囲で使う計算は、四則演算と、負の符号のカッコの外し方、累乗の数の計算、あとは分数が出たときの通分あたりかなあと思います。
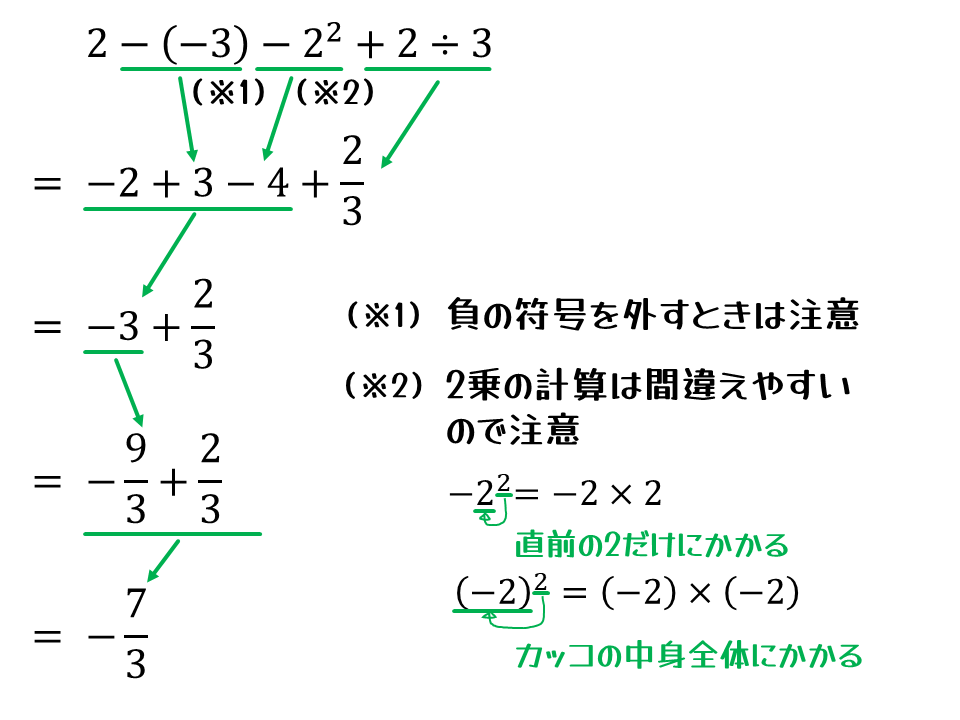
上の図の通り、途中計算を書くことは、基礎計算の復習にもなります。さらに、この効果を大きく活かそうと思うと、”6~7割程度は解ける問題集”を使うのがおすすめです。別記事でも取り扱ったので、興味があれば読んでみてください。
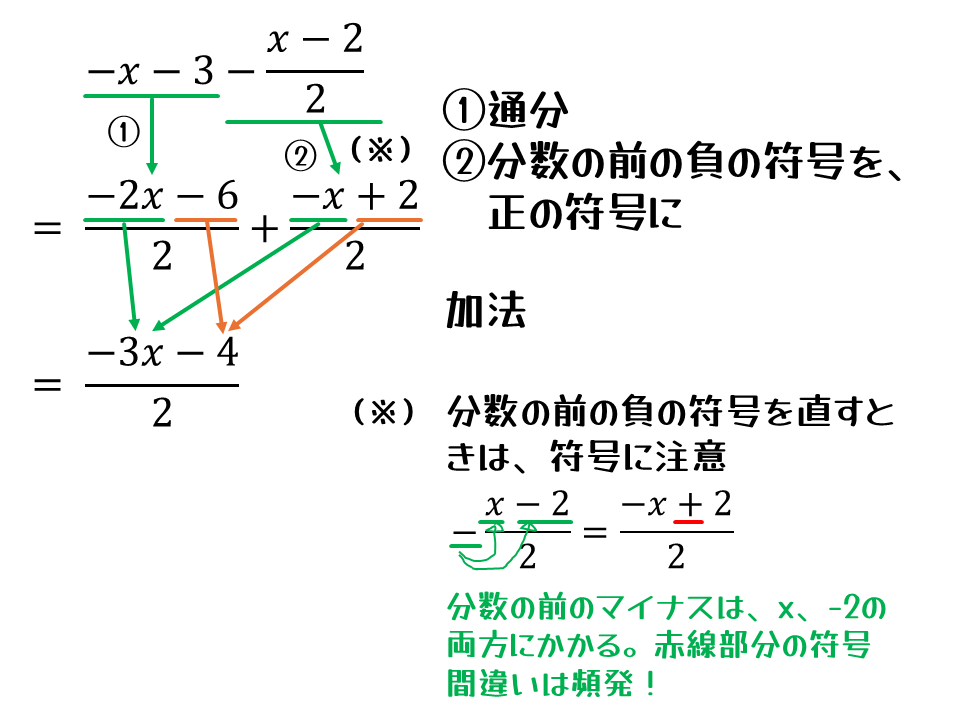
文字式の計算
文字式の計算だと、こんな感じです。特に、カッコや分数の前にある負の符号の処理は計算ミス頻発地帯なので、そこを計算したときは必ず途中計算を書いてください。
方程式
移項と、両辺に同じ数をかけたり、割ったりが、方程式(というか等式)特有の計算です。移項とその後の足し算、引き算ぐらいは一緒に書いてもいいです。苦手なら分けておいた方が無難です。
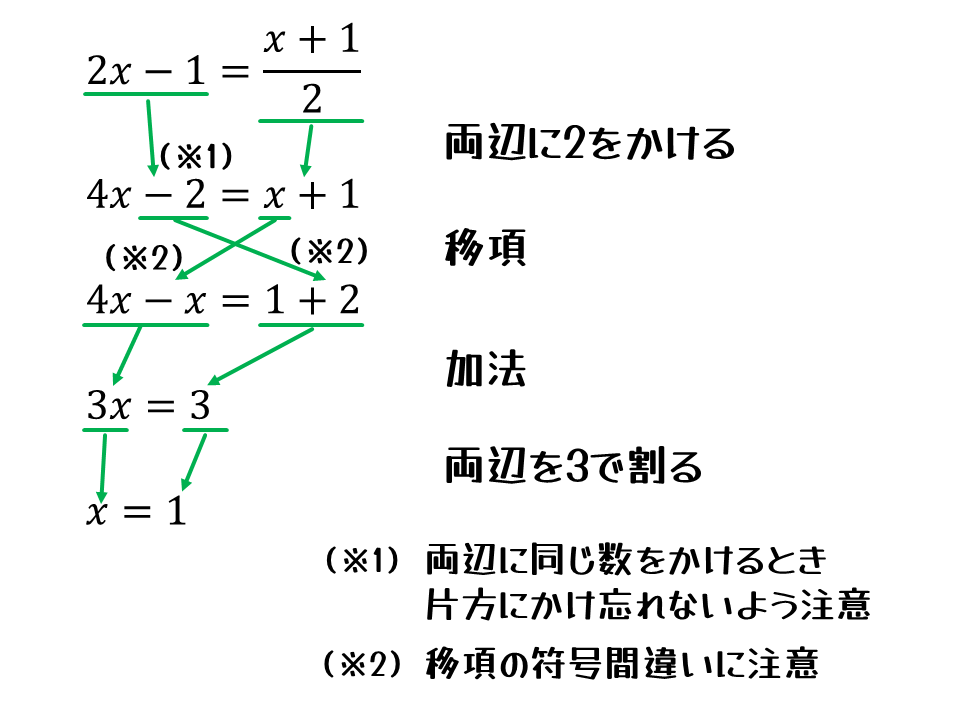

塾講師のときは、数学が苦手なクラスでは、復習の意味も込めて移項を別に書いてました。得意なクラスでは、授業のテンポが悪くなるので省略していました。何をどこまで書くべきかの基準はありません。だから、書くべきかどうか迷うときは、自分が間違えやすいかどうかで考えるといいです。
おわりに
今回の記事では、途中計算の書き方について説明しました。
途中計算の書き方のルールは
が基本です。ここからスタートして、演習を重ねてみてください。絶対の基準はないので、迷うときは「自分が間違えないように」を基準にしてみてください。
途中計算がよくなると、テストの点数も、勉強の効率もぐっと良くなります。最初は難しいかもしれませんが、こつこつと習慣にしていくと意識しなくても書けるようになるので、がんばってください。



コメント