因数分解でつまいた人へ：考え方の4ステップ

という人向けの記事です。

この記事では、因数分解の目的や基本のポイント、そして「どの公式をどう選べばいいか？」という考え方まで、背景にある考え方も含めて、わかりやすく解説していきます。

因数分解は、高校に進んでからもよく出てくる重要な内容です。
だからこそ、中学校の範囲は今のうちにしっかりマスターしておくことが大切です！

そもそも因数分解って何？

因数分解とは、数学において多項式や数式を、2つ以上の単項式や多項式の積の形に表すことです。平たく言うと、式を変形して、足し算、引き算をなくして、かけ算だけの式にすることをです。例えば

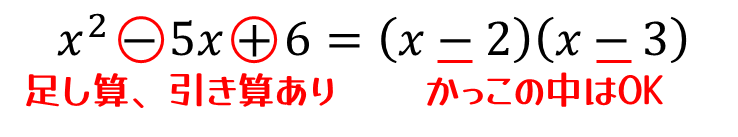
みたいなやつです。かっこの中身は、それで1つの数字という扱いなので中に足し算・引き算があってもかまいません。

なぜ因数分解をするのか

それは、式を因数分解することで考えやすくなることが多いからです。

例えば、「かけて6になる」整数の組み合わせを考えてみましょう。
候補は、(-1, -6)、(-2, -3)、(1, 6)、(2, 3)のように、限られた数しかありません。
でも「足して6になる」組み合わせは、(1, 5)、(2, 4)、(3, 3)、(6, 0)、(7, -1)、(8, -2)…と、いくらでも出てきます。このように、因数分解をして「かけ算の形」に直すと、検討すべきパターンがぐっと少なくなって、ずっと楽になるのです。

実はこれ、日常生活でもよく使う考え方です。何かの問題に向き合うとき、「とにかく全部考える」のではなく、「候補を絞り込みやすい形に整理し直す」ことってありますよね？因数分解は、数学におけるそのための“道具”なんです。

このあと学ぶ「二次方程式を解く」場面でも、因数分解は大いに役立ちますよ。

因数分解の基本公式

おさらいですが、因数分解の公式は以下の5つです。

1. \(ma+mb=m(a+b)\)
2. \(x+(a+b)x+ab=(x+a)(x+b)\)
3. \(x+2a+a^2=(x+a)^2\)
4. \(x-2a+a^2=(x-a)^2\)
5. \(x^2-a^2=(x+a)(x-a)\)

中学校で習う範囲では、すべての式が必ず因数分解できるわけではありません。
また、使える方法（やり方）は基本的に「公式」しかありません。

つまり、「因数分解しなさい」という問題が出されたときには、「その式は、必ずどれかの公式を使えば因数分解できる式になっている」という前提があるんですね。

なので、「この式は公式のどれにあてはまるかな？」と考えてみることが、因数分解の第一歩になります。

どの公式を使えばいいか？：因数分解の考え方4ステップ

ただ、どの公式を使えばいいのかを見分けるときにも、実は“考える順番”があります。

基本の公式をちゃんと覚えていて、公式ごとに分けられた問題なら解ける人でも、
いろいろなパターンが混ざると急に解けなくなったり、時間がかかってしまったりすることがあります。これは、「どの順番で考えればいいか」があいまいになっているからなんですね。

もちろん、たくさん問題を解いていけば、だんだん慣れて自然にできるようになります。
でも、最初のうちはその“順番”を意識しながら取り組んだ方が、もっと早く上達できますよ。

具体的には、次の4つのステップで考えればOKです。

1. まず、共通因数でくくれないかを考えます。
   これは「公式①」にあたります。すべての項に共通してかけられる数や文字がないかチェックしましょう。
2. 次に、\(x^2-a^2\)の形（公式⑤）になっていないかを確認します。
3. 定数項が「ある数の2乗」になっていないかを見てみましょう。
   もしそうなら、\(x\)の係数が定数項の2乗する前の数字（平方根といいます。例えば、4の平方根は2か-2、16の平方根は4か-4です。因数分解の後に詳しく習います。）の2倍になっていないか確認しましょう。これが当てはまれば、公式③または④が使えます
4. 上の1〜3のどれにも当てはまらなければ、最後に使えるのは公式②だけです。

「え？この順番、学校で習った順番と違う…」
と、思った人もいるかもしれませんね。

実はこれ、苦手な人がひっかかりやすいポイントなんです。
学校では公式①から順番に学ぶので、その順に使いたくなるんですが、実際の問題ではそううまくはいきません。

ここで紹介している順番には、ちゃんとした理由があります。

それは、

• 見てすぐにわかりやすい形から先にチェックする
• 当てはまるパターンが少ないものを先にしぼる
• 最後に残ったものに当てはめてみる

というふうに、「選択肢をしぼりながら考える」というやり方になっています。これは、数学だけじゃなくて、いろんな問題に向き合うときによく使われる考え方の整理の順番なんですよ。

では、実際の問題で見てみましょう。

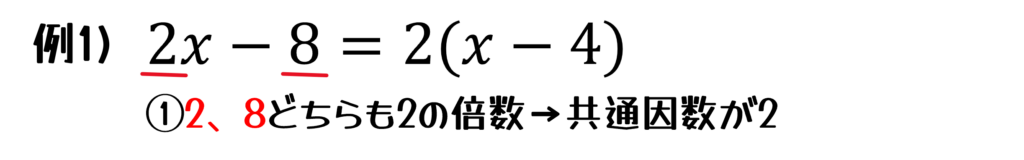
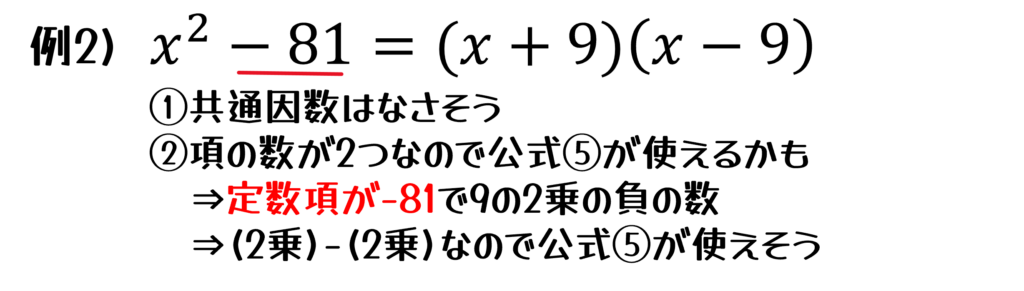
計算に慣れてくると、公式⑤や公式③・④が使えるかどうかは、パッと見ただけでわかるようになってきます。

でも、それまでは今回の「4つのステップ」を意識して取り組むことで、演習がぐんとやりやすくなると思います。

終わりに

少し前に、タレントの出川哲朗さんが「因数分解なんて、一生使わないよ！」みたいなことを言っていました。
たしかに、多くの人は受験が終わったあと、因数分解を直接使う機会はほとんどありません。

でも、因数分解の公式を使うときの「わかりやすいものから考える」「候補の少ないものから先に試す」といった考え方や、そもそも因数分解をする目的である「式をシンプルにして、見通しをよくする」という考え方は、これからの人生の中で、きっとどこかで役に立つ場面が出てきます。

だからこそ、ただ公式を丸暗記して終わりにせず、その背景にある考え方までしっかり身につけていってくださいね。