「二次関数のグラフ、フリーハンドで描くのが難しそう…」と不安に思っていませんか?
どこまで点を打ち、どこまで線を伸ばせばいいのか、実は迷うポイントはみんな同じです。
でも、コツはたったの2つ。
「整数の点をとる」ことと、「滑らかにつなぐ」ことだけ!
この記事を読めば、5分できれいな放物線が描けるようになります。
さっそく、一番かんたんな描き方をマスターしましょう!
【関連記事】
- 前回の記事を読まれる方はこちら
二次関数の基本操作、\(x,y\)の求め方や、式の求め方についてまとめました。
計算ミスしやすい点や、ミスを減らす練習方法についても詳しく解説しています。
テストの点数アップにも、応用問題を解くにも必須の知識ですので、ぜひ読んでみてください。
👉二次関数、ポイントは式への代入!x,yの計算と式の決定
二次関数のグラフってどうやって描いたらいい?
二次関数\(y=ax^2\)のグラフは、次の手順で描くことができます。
二次関数のグラフは直線ではないため、一次関数のように「2点だけとってグラフを描く」というようなことはできません。
そのため、通る点をとって滑らかにつないでグラフを描きます。
ここから、\(y=2x^2\)のグラフを例に、各手順について詳しく見ていきます。
ステップ1:整数の点をとる
まずは整数の点\(x, y\)をとります。
慣れないうちは表を作ると整理しやすいです。
\(y=2x^2\)であれば、次のように表を埋めていきます。
今回は、\(a\)(比例定数)が整数なので、\(x\)は小さい順に整数を代入していけばいいので、
\(x=0, \pm 1, \pm 2,…\)と埋めていきます。
グラフ用紙内にある整数の点は全部計算して点を打ってください。
定期テストでは、\(y\)座標が-10~10の範囲内の用紙が多いので、
\(y\)の絶対値が10以内のものを計算すれば大丈夫です。
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | 8 | 2 | 0 | 2 | 8 |
計算できたら、グラフ用紙に正確に打ちます。
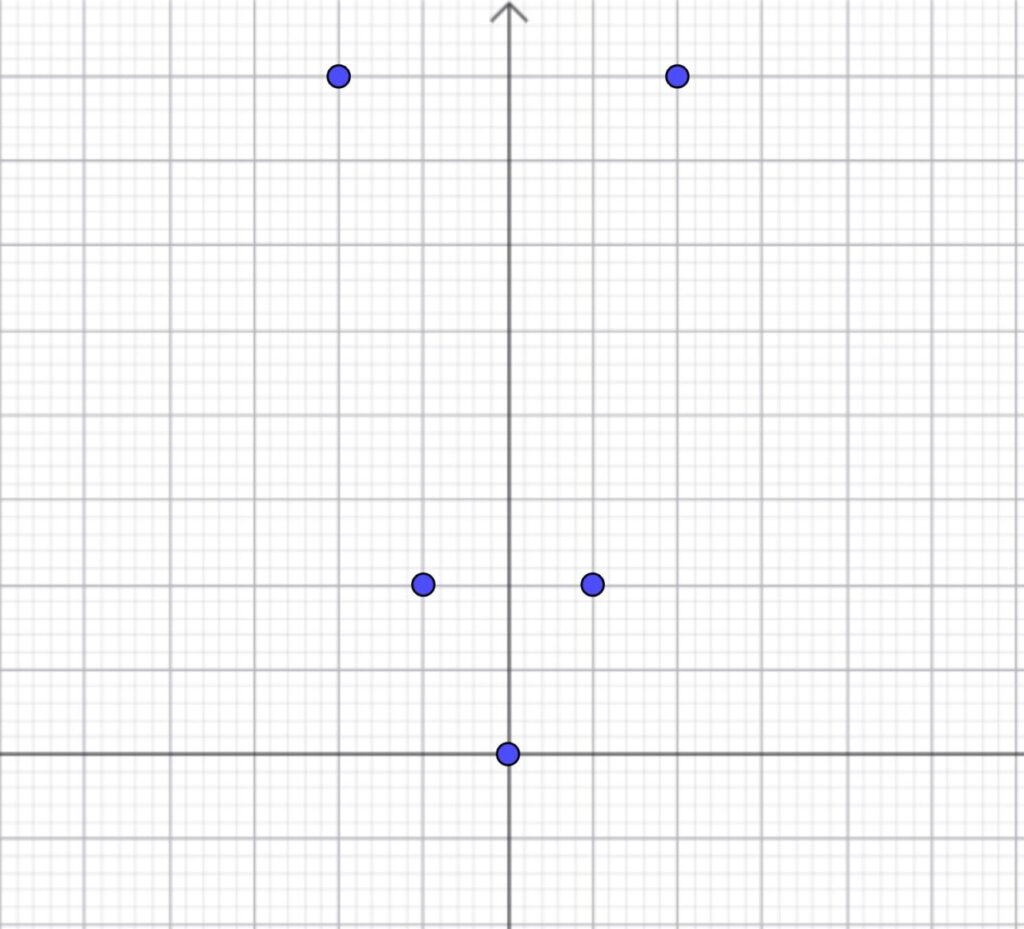

\(a\)の値が分数のときは、\(y\)の値を整数にするためには\(a\)の分母を消さなければいけません。
そのため、\(x\)の値は、\(a\)の分母の倍数だけを考えていけばいいです。
ステップ2:滑らかな曲線でつなぐ(仕上げ)
打った点を通るように、フリーハンドで滑らかな曲線を引きます。
そのとき、以下の点を意識すると書きやすいです。
- 一筆書きにこだわらない:
「頂点(原点)から右上」に、次に「頂点から左上」に、と
2回に分けて外側に向かって描くと形が整いやすいです。 - 「U字」を意識::
原点付近はカクッとさせず、少し丸みを持たせます。 - 端まで描く:
最初にとった、整数の点の最後の点で止まってしまう人がときどきいます。
そこを通り過ぎて、グラフ用紙の端(枠線の際)まで線を伸ばしましょう。
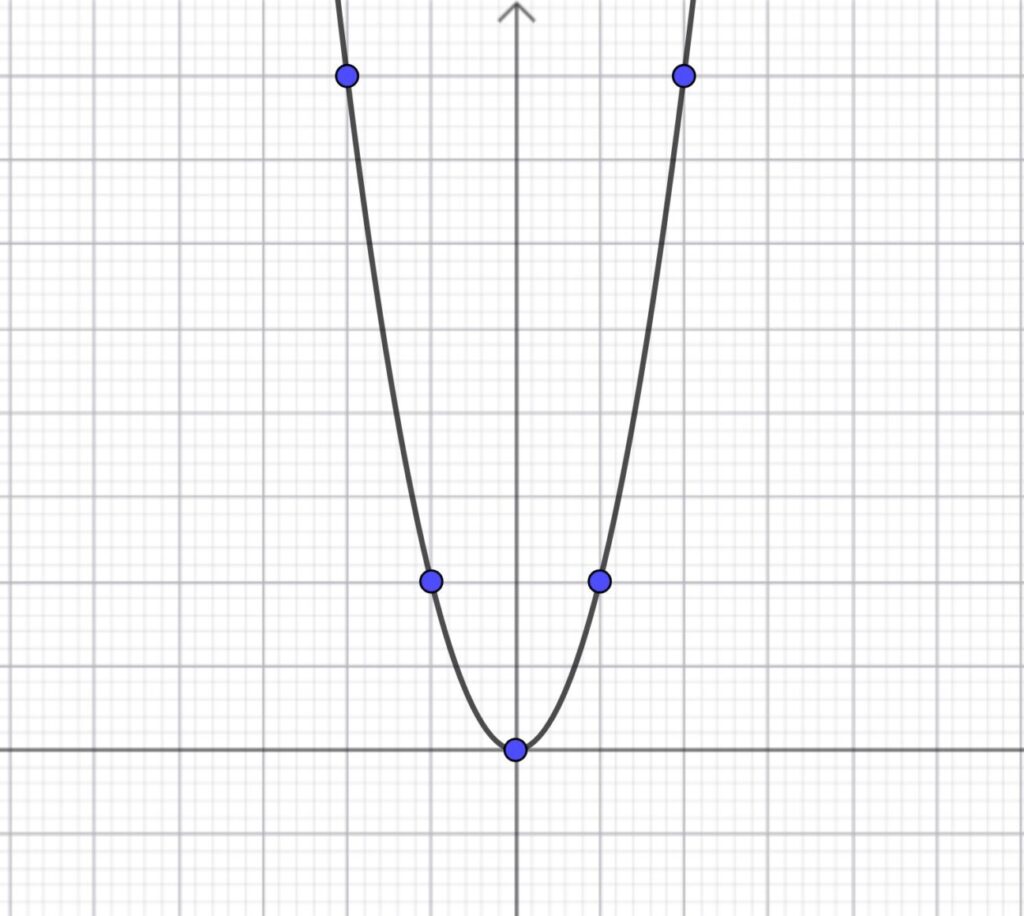
二次関数のグラフは、物を投げたときの落下の軌道と同じになります。
そのため、二次関数のグラフは「放物線」とも呼ばれます。

二次関数のグラフは、ボールを投げたときの軌道と同じ形をしています。
だから、数学ではこのカーブを 「放物線(ほうぶつせん)」 と呼びます。
文字通り「物を放り投げたときの線」という意味ですね。
ちなみに、なぜ投げた物がこの形になるのかは、高校の物理で詳しく習います。
「現実の世界の動きが数学で習った式で表される」ことを実感できる面白い分野ですよ。
補足:\(x,y\)の値とグラフの形の関係
ここで、計算した表の数字をじっくり見てみてください。
グラフがなぜになる秘密が隠されています。
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | 8 | 2 | 0 | 2 | 8 |
左右がピッタリ重なる理由
\(x=1\)と\(x=-1\)のときや、\(x=2\)と\(x=-2\)のときのどちらも、\(y\)の値はそれぞれ同じです。
\(y=ax^2\)の\(x\)の式では\(x\)を2乗するため、
\(x\)の符号が違っても、絶対値が同じであれば\(y\)の値は同じになるのです。
そのため、\(y=ax^2\)のグラフは\(y\)軸を折り目にして「左右対称」になるのです。
このような関係を「\(y\)軸に関して線対称である」と言います。
カーブがどんどん急になる理由
\(y\)の増え方に注目すると、\(x\)が
\(0→1\)のときは「\(2\)」しか増えていないのに、
\(1→2\)のときは「\(6\)」も増えています。
だから、グラフは直線ではなく、後にいくほど跳ね上がるカーブ(放物線)になるのです。
なぜ、点を打って線でつなげばグラフが描けるの?
点を打って、線をつなぐとグラフが描けるのは、
実は、関数のグラフの正体は「点の集まり」だからです。
今は、\(x=0, \pm 1, \pm 2\)のように整数の点しか打っていませんが、
その間にある\(0.1\)や\(0.01\)の点も全部打っていくと、
最終的に一本のきれいな線になります。
線は無数の点を代表しているだけなのです。
「なんで式から線ができるの?」と不思議に思った方は、こちらの記事で詳しく解説しています!
👉 関数のグラフっていったい何?意味と仕組みをやさしく解説
おわりに
お疲れさまでした!
二次関数のグラフを描くポイントは、次の3つです。
- 整数の点をできるだけ多く打つ
- 頂点(原点)から外側へ向かって2回に分けて描く
- 最後は点で止めず、用紙の端まで伸ばす
この基本さえ守れば、もうグラフは怖くありません。
次は、比例定数\(a\)の値でグラフがどう変わるのか、4つの例題でチェックしていきましょう!
【関連記事】
- 続きの解説記事を読まれる方はこちら
今回学習した二次関数のグラフの形が、\(a\)の値によってどう変わるのかについてまとめた記事です。
また、\(a\)の数字が同じで符号が違う2つのグラフの関係性についてもまとめています。
二次関数のグラフへの理解がもっと深まると思うので、ぜひ読んでみてください。
👉二次関数のグラフの形はaで決まる!開き方と向きの違いを例題で解説


コメント