「二次関数のグラフって、描き方はわかったけど\(a\)が変わるとどうなるの?」
「テストで『開き方が大きい順に並べなさい』って言われると混乱する……」
そんな悩みを持っていませんか?
二次関数の式の\(a\)の部分には、グラフの向きと開き具合を決めるという、とても重要な役割があります。
この記事では、4つの例題を使って、\(a\)の値によってグラフがどう変化するのかを視覚的に解説します。
「暗記」ではなく「なぜそうなるのか?」という仕組みから理解して、グラフの性質を完璧にマスターしましょう!
【関連記事】
- 前回の記事を読まれる方はこちら
二次関数のグラフの描き方に自信のない方や、どうやったらきれいにグラフを描けるのかを知りたい方はこちらの記事をお読みください。
関数のグラフの意味からはじめて、二次関数のグラフの形の特徴、そうなる根拠までを解説しています。
👉二次関数のグラフの描き方|5分で克服!きれいに描く2ステップとコツ
\(y=ax^2\)の\(a\)の違いでグラフはどう変わるの?
二次関数のグラフは、\(a\)の符号と\(a\)の絶対値の大小で、次のように変わります。
それぞれ、例題を見ながら確認していきましょう。
使用するグラフ用紙は、\(y\)の最大値が10、最小値が-10の次のグラフ用紙です。
\(a\)の符号による違い
【例題1】
\(y=x^2\)のグラフを描きなさい。
【解説】
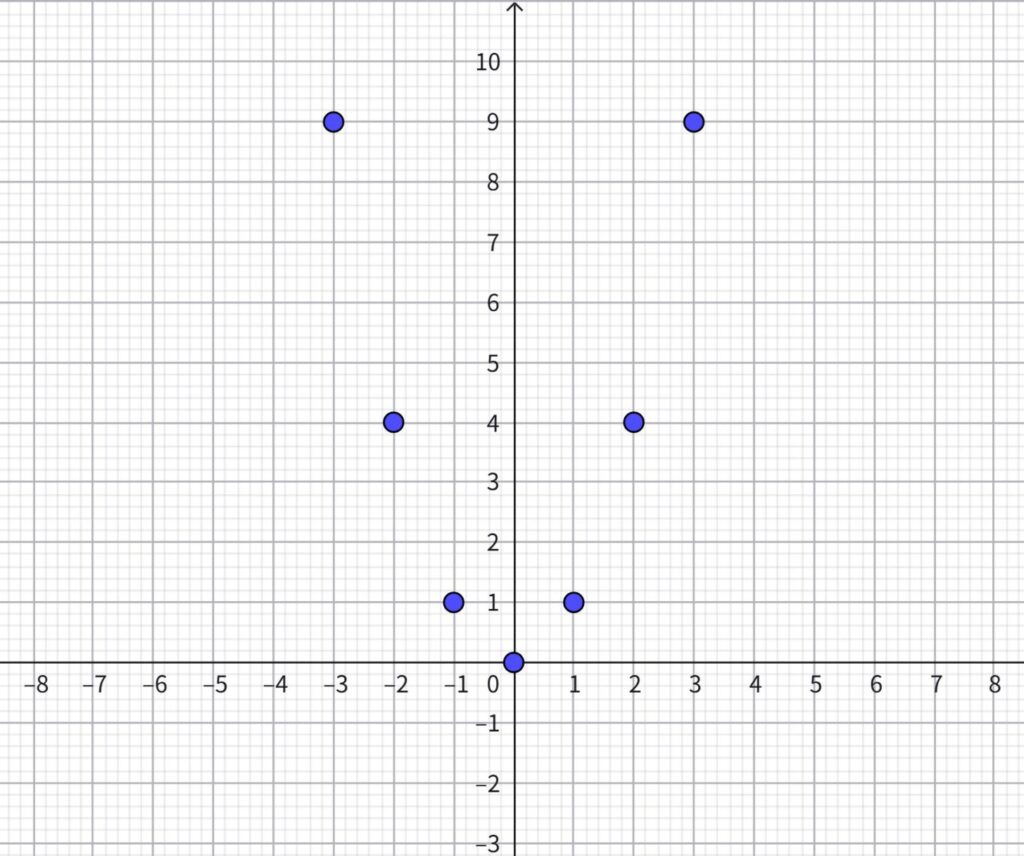
まず、グラフ上にあるすべての整数の点をとる。
整数の点は下の表の通り。
| \(y\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(x\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
この点を、グラフ用紙にとると次の通り。
この7点を通る滑らかな曲線を引くと、グラフは次のように描ける。
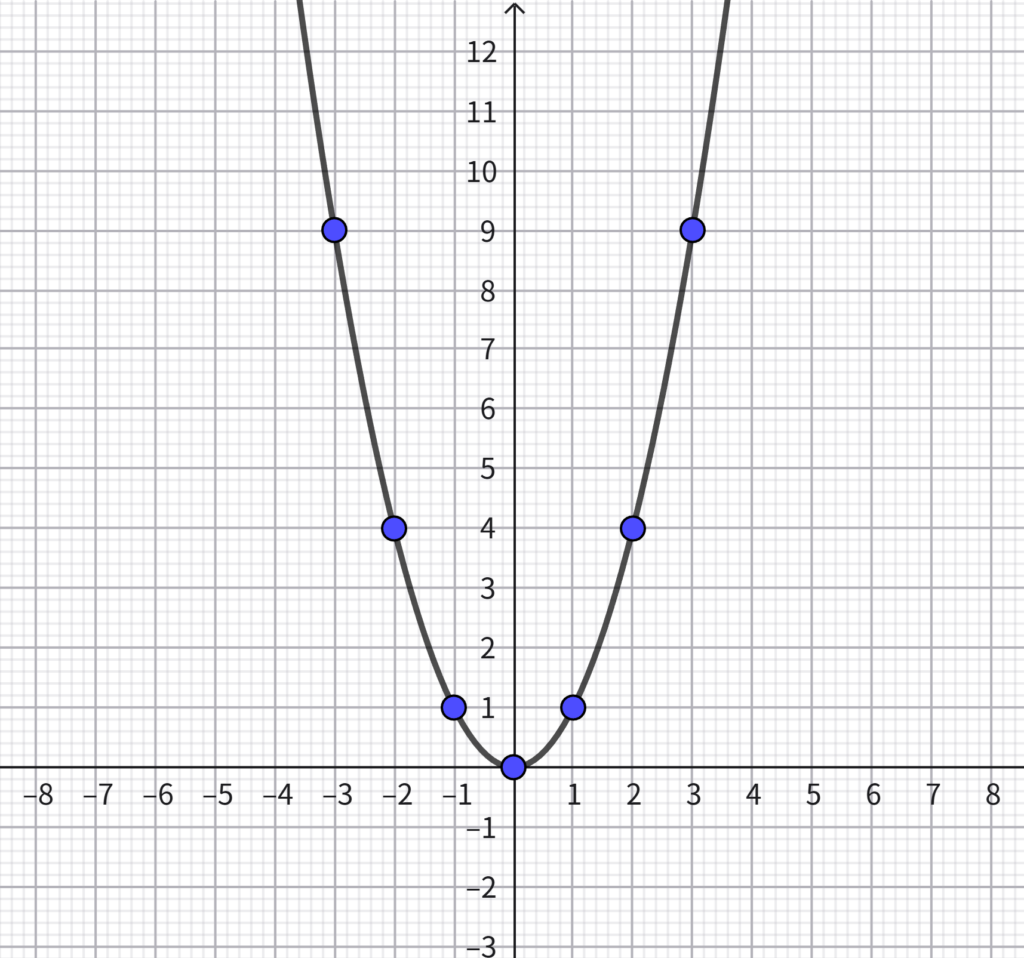

今回、グラフ用紙の最大値が10までなので、
\(x= \pm 3\)(\(y=9\))まで計算しています。
グラフが通る整数の点はすべて通る必要があるので、必ずすべて点を打ってください。
【例題2】
\(y=-x^2\)のグラフを描きなさい。
【解説】
まず、グラフ上にあるすべての整数の点をとる。
整数の点は下の表の通り。
| \(y\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(x\) | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
この点を、グラフ用紙にとると次の通り。
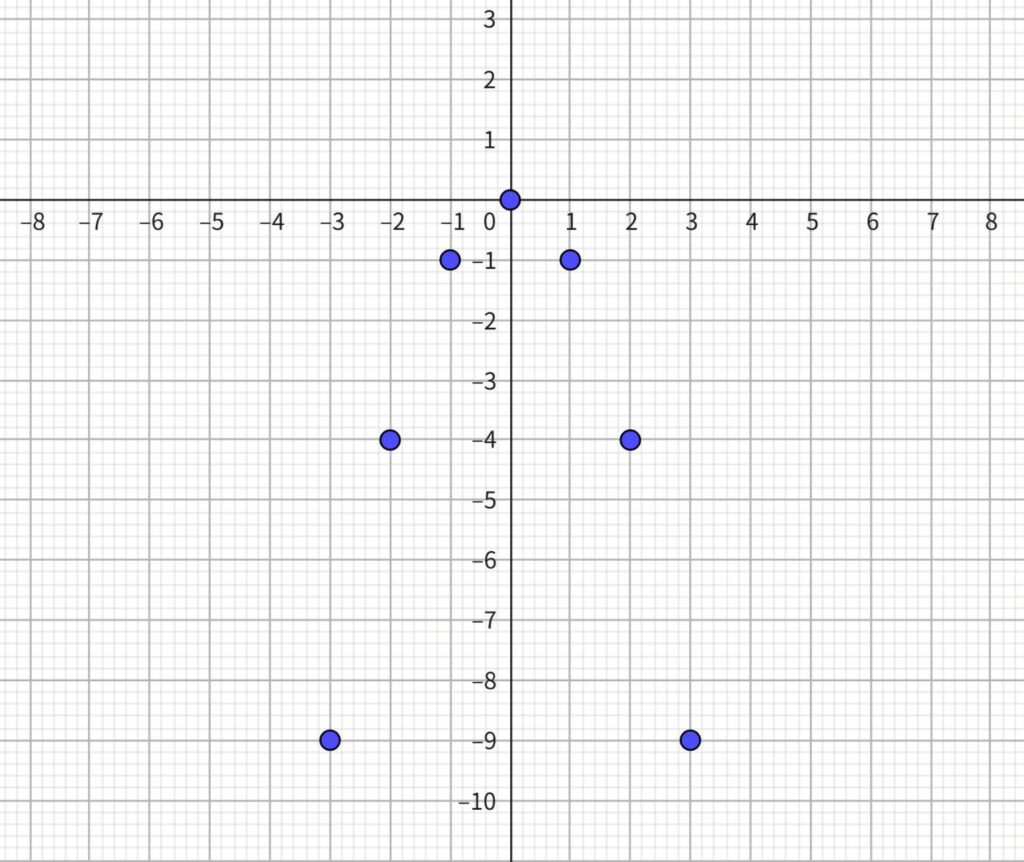
この7点を通る滑らかな曲線を引くと、グラフは次のように描ける。
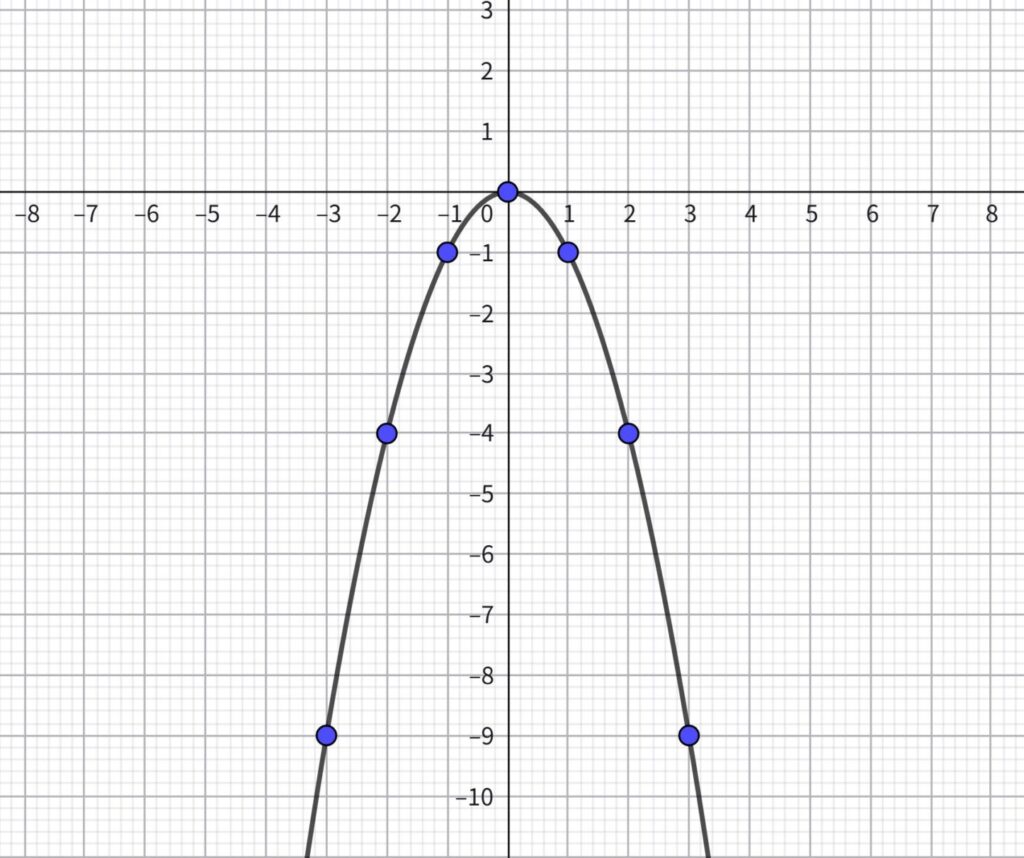
\(y=ax^2\)の式では、\(x^2\)が常に0以上であるため、次のことが言えます。
- \(a\)>0のとき
\(x\)の値がいくつでも、常に\(y>0\)(グラフ用紙の上側)に点がくる
⇒グラフは原点を頂点として、\(y>0\)の領域に広がる - \(a\)<0のとき
\(x\)の値がいくつでも、常に\(y>0\)(グラフ用紙の下側)に点がくる
⇒グラフは原点を頂点として、\(y>0\)の領域に広がる
\(a\)の絶対値の大小による違い
【例題3】
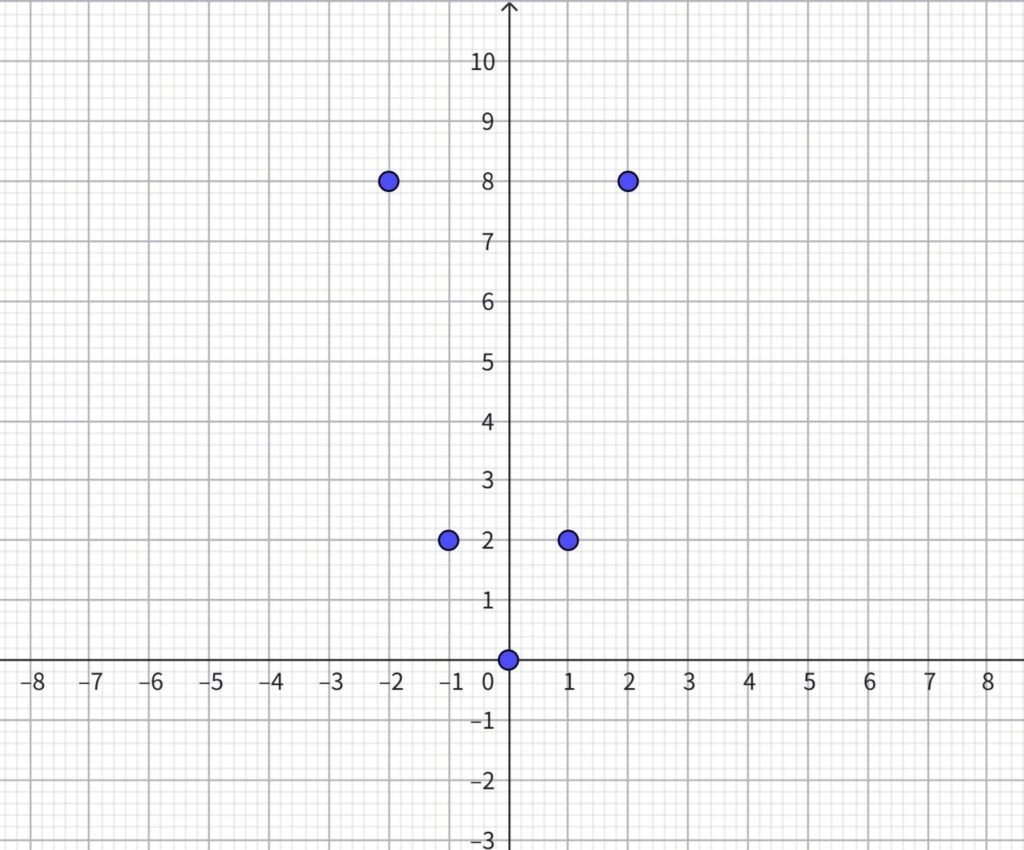
\(y=2x^2\)のグラフを描きなさい
【解説】
まず、グラフ上にあるすべての整数の点をとる。
整数の点は下の表の通り。
| \(y\) | -2 | -1 | 0 | 1 | 2 |
| \(x\) | 8 | 2 | 0 | 2 | 8 |
この点を、グラフ用紙にとると次の通り。
この3点を通る滑らかな曲線を引くと、グラフは次のように描ける。
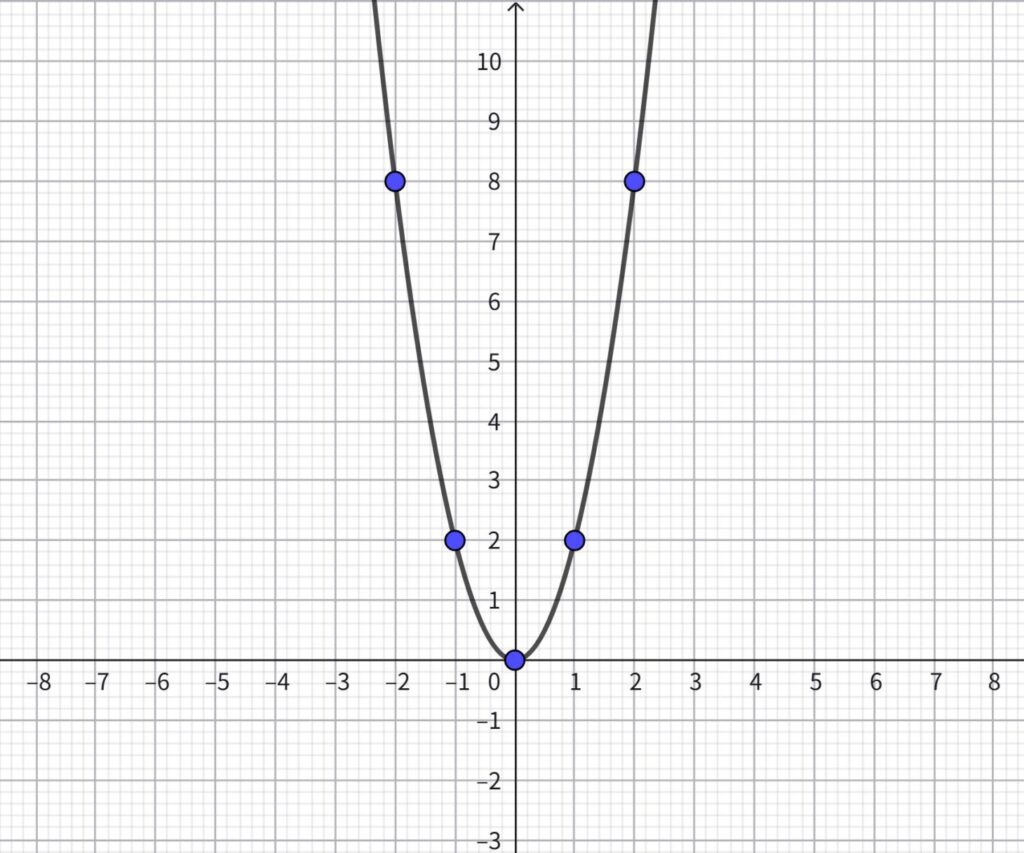
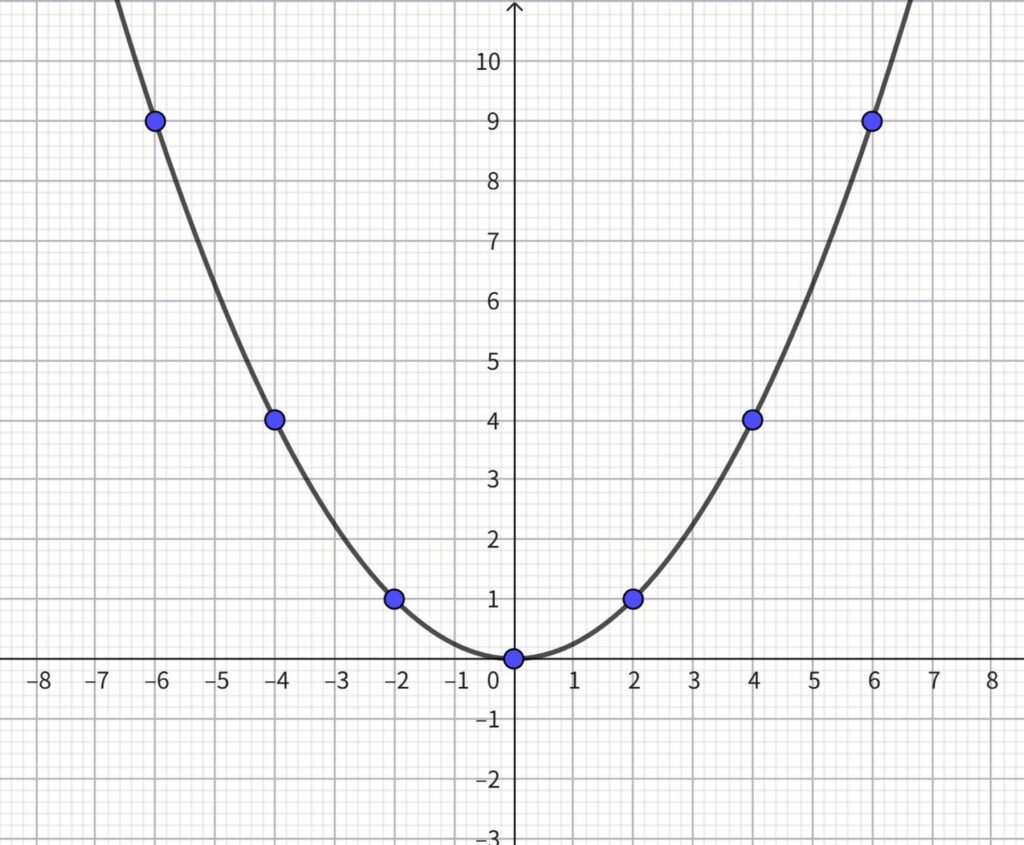
【例題4】
\(\displaystyle y =\frac{1}{4}x^2\)のグラフを描きなさい。
【解説】
まず、グラフ上にあるすべての整数の点をとる。
整数の点は下の表の通り。
| \(y\) | -4 | -2 | 0 | 2 | 4 |
| \(x\) | 4 | 1 | 0 | 1 | 4 |
この点を、グラフ用紙にとると次の通り。
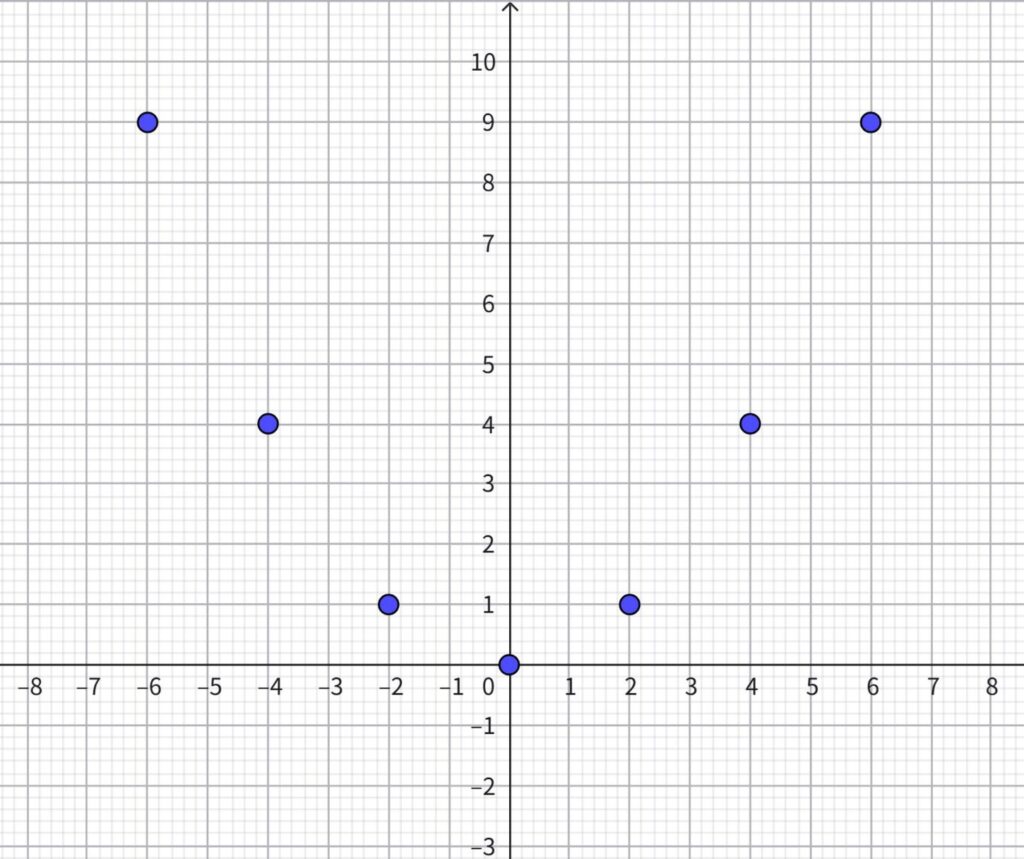
この5点を通る滑らかな曲線を引くと、グラフは次のように描ける。

\(a\)の値が整数のときは、\(x\)の値を(\(\pm 1,\pm 2,…\))と順に代入すればよいですが、分数のときは分母と約分できる\(x\)だけを代入していくとよいです。
\(a>0\)のときで考えます。
\(a\)の絶対値が大きい方が、\(x\)が増加に対する\(y\)の増加量が大きいです。
そのため、同じ\(x\)の値に対する\(y\)の値は、\(a\)の値が大きい関数の方が大きくなります。
そして、それをグラフ上で表現すると、グラフは上側にくることになるのです。
すべての\(x\)において、\(a\)の値が大きいグラフの方が上側に来るので、結果として\(a\)の値の大きいグラフは狭くなるのです。
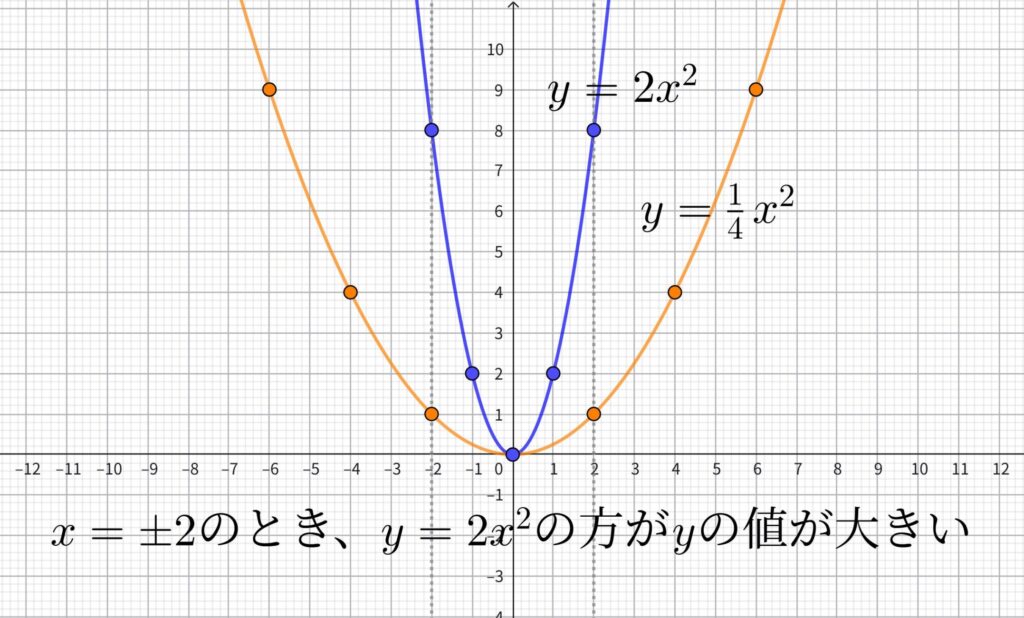
そのため、\(a\)の絶対値が大きい式の方が、グラフは狭くなるというわけです。
\(a<0\)のときも、同様の理由で、\(a\)の絶対値が大きい方がグラフは狭くなります。
\(a\)の数字が同じで、符号が逆のグラフ同士の関係は?
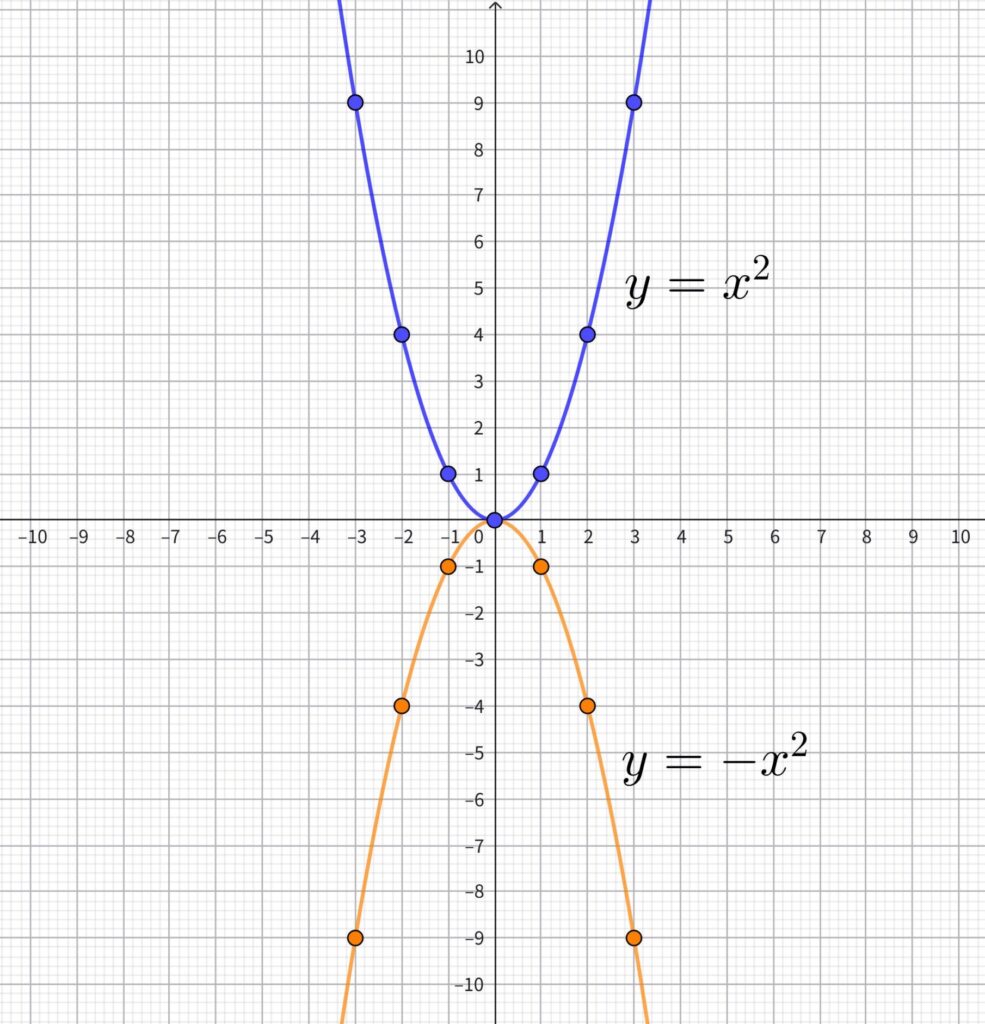
例題1と例題2の比較でグラフの関係性を確認しよう
前の例題1と例題2のグラフを見比べてください。
\(y=x^2\)と\(y=-x^2\)のグラフでは、
\(a\)の符号が正と負で、数字の大きさが同じです。
つまり、2つのグラフは、開き具合が同じで、原点を頂点として上下逆に開いていくグラフになります。
そのため、2つのグラフは\(x\)軸で折ると、ぴったり重なるのです。
このような関係を「\(x\)軸に関して線対称である」と言います。
また、この2つのグラフは原点を中心に180°回転させてもぴったり重なります。
このような関係を「原点に関して点対称である」と言います。
おわりに
お疲れ様でした!
二次関数のグラフにおける\(a\)の役割を整理すると、ポイントは2つだけです。
- 符号(プラス・マイナス)
グラフが「上」に開くか「下」に開くかを決める - 絶対値(数字の大きさ)
数字が大きいほど、グラフは「シュッと狭く」なる
また、「対称性」の話も、とても大事です。
「\(x\)軸で折ったら重なる」「180度回しても重なる」ということを、
頭の中でしっかりイメージできるようにしておいてください。


コメント