一次関数のグラフって、分数の傾きや切片が出てくると一気に難しく感じませんか?
今回の記事では、そんなつまずきをなくすために、関数のグラフを練習できる演習ページを用意しました。
このページでは、一次関数のグラフを 6つの演習問題で総合的に練習できます。
傾き・切片が整数の場合から、分数をふくむ少しむずかしいタイプまで、テストによく出るパターンをまとめて確認できるようにしています。
理由を意識しつつこの問題をくり返していけば、グラフの描き方は自然と身についていきます。
一緒に丁寧にステップアップしていきましょう。
【関連記事】
- 「切片⇒傾き」の順で考える基本的な一次関数の描き方に自信のない方はこちら
「切片⇒傾き」で考えるグラフの基本的な描き方についてまとめました。
ほとんどのグラフはこの方法で描くことができます。
👉「切片⇒傾き」で考える!一次関数のグラフ、基本の描き方 - 切片が分数のグラフの描き方に自信がない方はこちら
切片が分数であるグラフを描くコツは、1点目の取り方を工夫することです。
具体例付きで、切片が分数のグラフの描き方についてまとめています。
👉一次関数グラフの描き方、切片が分数のグラフは1点目の取り方を工夫!
一次関数のグラフってどう描けばいい?
一次関数のグラフは通る2点をとって線を引く
一次関数のグラフを描く手順は以下のようにまとめられます。
これで、傾き、切片が分数でもすべて描くことができます。
よくあるミス
この範囲でよくあるミスは、点の読み間違いです。
たとえば、格子を読み間違えて、
「点(0, 3)をとりたかったのに、点(0, 2)をとってしまった」
というミスはよく起こります。
グラフは、原点、軸がとても大事です。
最初に、原点、\(x\)軸、\(y\)軸をしっかり確認して正しい位置に点を打つようにしましょう。
また、切片が分数のときの一次関数のグラフの描き方は、テスト当日に抜けやすいです。
しっかり手順を確認しておきましょう。
一次関数のグラフの描き方の演習

どのパターンでも描けるようになってほしいので、あえてパターンをばらばらにしています。
1つずつ手順を確認しながら演習してみてください。
演習1
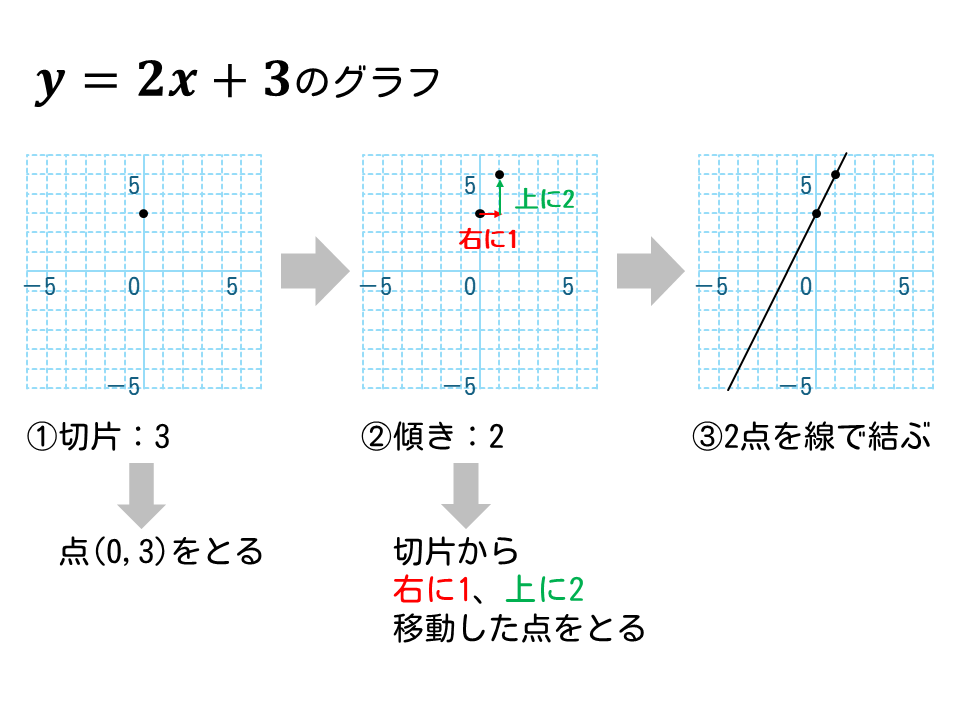
\(y=2x+3\)のグラフを描きなさい。
解説
- 最初の点
切片が3
⇒点(0, 3)をとる - 次の点
傾きが2
⇒最初のから右に1、上に2移動した点をとる - 2つの点を線で結ぶ
解答は下図の通り
演習2
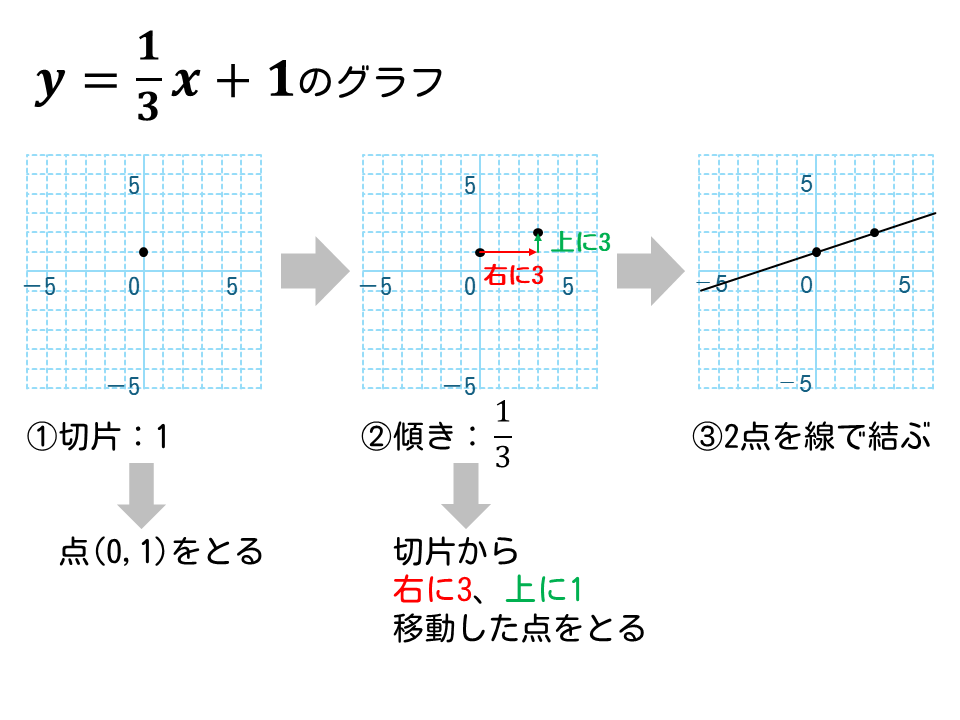
\(\displaystyle y=\frac{1}{3}x+1\)のグラフを描きなさい。
解説
- 最初の点
切片が 1
⇒点(0, 1)をとる - 次の点
傾き\(\displaystyle \frac{1}{3}\)
⇒最初の点から右に3、上に1移動した点をとる - 2つの点を線で結ぶ
解答は下図の通り
演習3
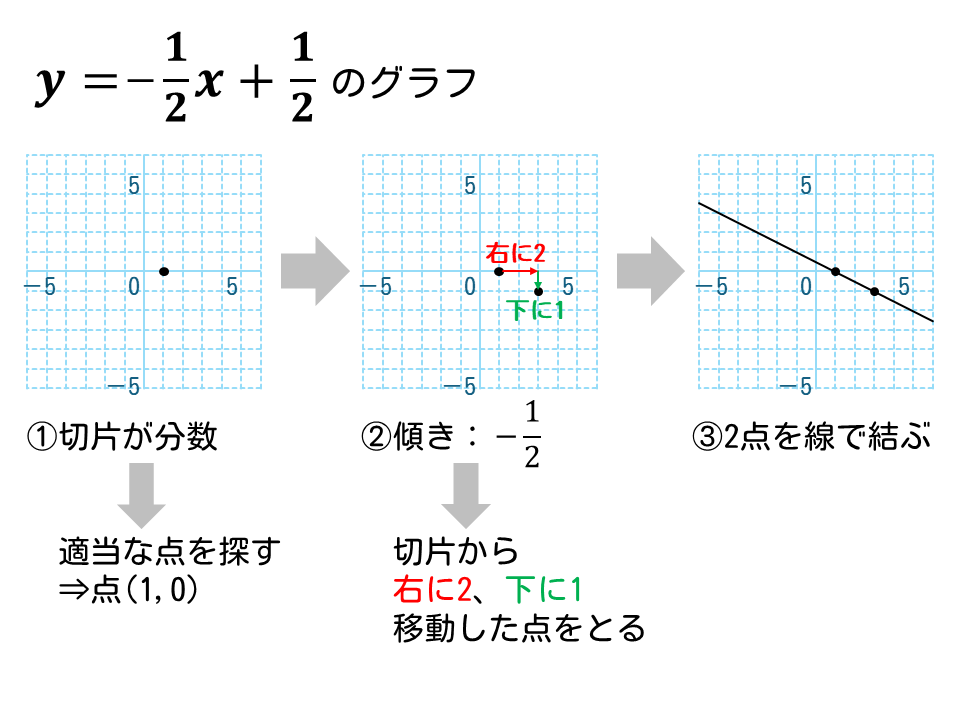
\(\displaystyle y=-\frac{1}{2}x+\frac{1}{2}\)のグラフを描きなさい。
解説
- 最初の点
切片が分数なので、適当な点を探す
⇒\(x=1\)のとき、\(y=0\)
⇒点( 1, 0 )をとる - 次の点
傾き(\displaystyle -\frac{1}{2}\)
⇒最初の点から右に2、下に1移動した点をとる - 2つの点を線で結ぶ
解答は下図の通り
演習4
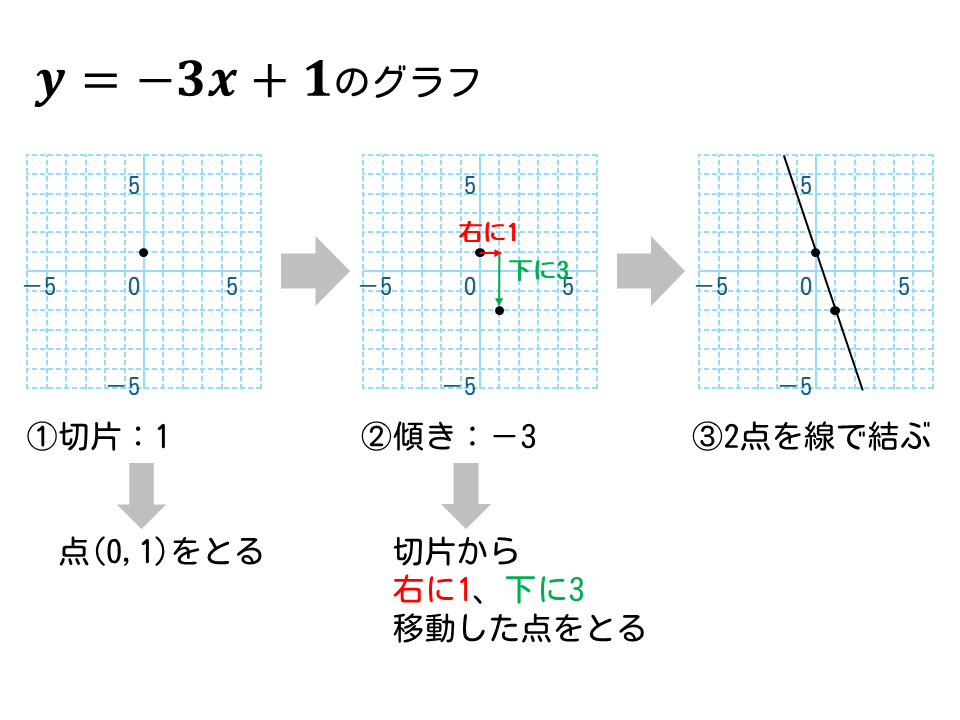
\(y=-3x+1\)のグラフを描きなさい。
解説
- 最初の点
切片が 1
⇒点(0, 1)をとる - 次の点
傾き(\displaystyle -\frac{1}{2}\)
⇒最初の点から右に2、下に1移動した点をとる - 2つの点を線で結ぶ
解答は下図の通り
演習5
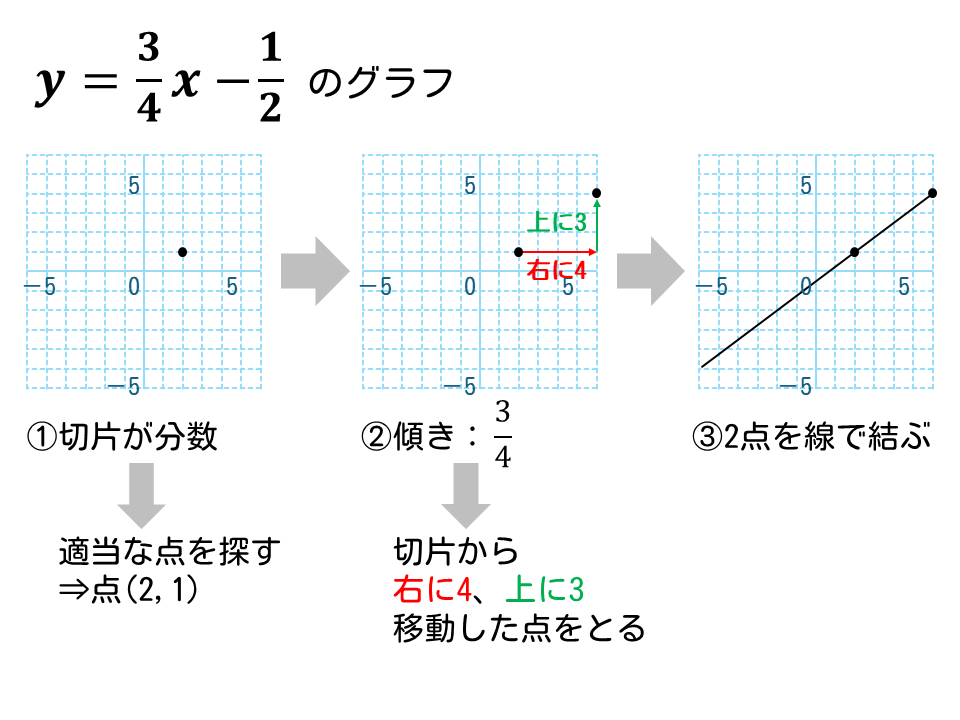
\(\displaystyle y=\frac{3}{4}x-\frac{1}{2}\)のグラフを描きなさい。
解説
- 最初の点
切片が分数なので、適当な点を探す
⇒\(x=2\)のとき、\(y=1\)
⇒点( 2, 1 )をとる - 次の点
傾き(\displaystyle \frac{3}{4}\)
⇒最初の点から右に4、下に3移動した点をとる - 2つの点を線で結ぶ
解答は下図の通り
演習6
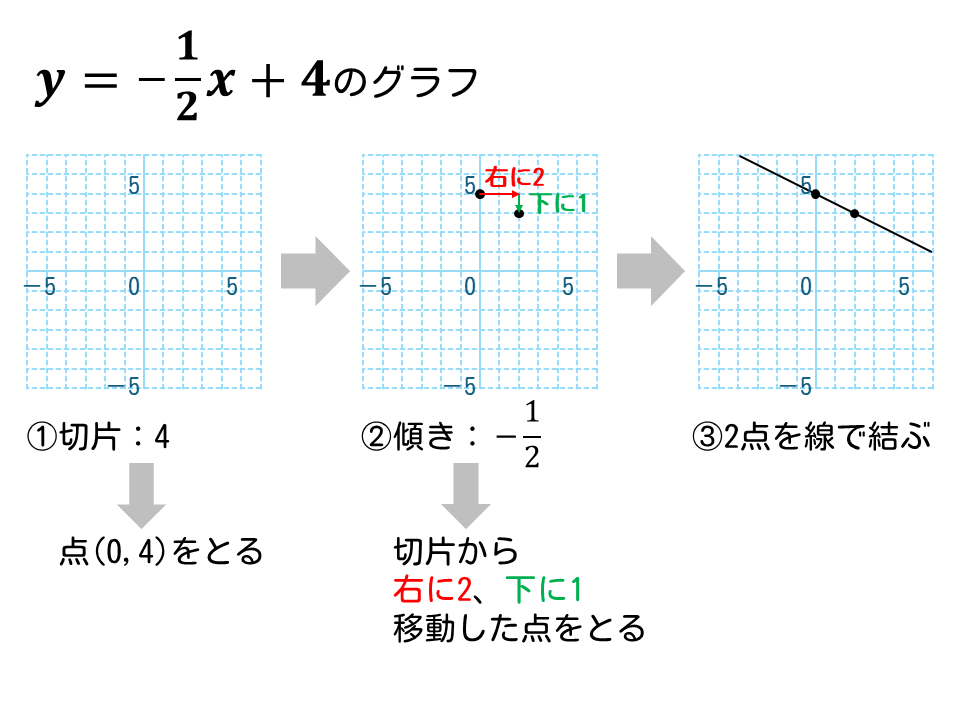
\(\displaystyle y=-\frac{1}{2}x+4\)のグラフを描きなさい。
解説
- 最初の点
切片が 4
⇒点(0, 4)をとる - 次の点
傾き\(\displaystyle -\frac{1}{2}\)
⇒最初の点から右に2、下に1移動した点をとる - 2つの点を線で結ぶ
解答は下図の通り
おわりに
今回は、グラフの描き方の演習についての記事でした。
傾き、切片が整数、分数と分けて覚えるより、一つの手順としてまとめておく方がいいと思います。
最初に学習するときは少し大変ですが、テスト当日に思い出しやすく、またテストが終わったあとも忘れにくいです。
また、グラフの描き方が定着したら、グラフからの関数の読み取りも続けて学習しておくとよいです。
全く同じ考え方で、「一次関数の式⇒グラフ」「グラフ⇒一次関数の式」と変換しているので、いっしょに勉強すると、一次関数の式とグラフの関係への理解がより深まります。
(だから解説記事はこの2つをまとめています)
グラフの理解が深まれば、何も考えずに描けるようになってくるので、少しずつでいいので、こつこつがんばってください。
【関連記事】
- 次の解説記事を読む方はこちら
直線の式のほとんどは一次関数ですが、例外が2つあります。
それが\(「x=a」,「y=b」\)のグラフです。
このグラフの意味や、グラフの描き方、直線のグラフの考え方などについて解説します。
👉一次関数ではない直線「x=a」「y=b」をていねいに解説 - この範囲の解説記事を読みたい方はこちら
「切片⇒傾き」の順で考える、一次関数のグラフの基本的な描き方についてまとめました。
グラフの基本を身に付けたい方はこちらの記事をお読みください。
👉「切片⇒傾き」で考える!一次関数のグラフ、基本の描き方
切片が分数のときの一次関数のグラフの描き方についてまとめました。
定期テスト以外での出題はほとんどないですが、定期テストではだいたい1題出ます。
描き方を押さえて得点アップしたい方はぜひお読みください。
👉切片が分数である一次関数のグラフの描き方 - 一次関数のまとめに戻る方はこちら
関数は、抽象的で取り組みづらい反面、同じ操作が繰り返し出てくるので、コツが掴めると得意にしやすい分野でもあります。
考え方からていねいに解説しているので、ぜひ先々まで活用できるかたちで知識を身に付けてください。
👉【完全攻略】一次関数の解き方・考え方を基礎からじっくり


コメント