連立方程式の加減法をマスター！レベル別演習【中2数学】

連立方程式の加減法は、中2数学の重要単元です。

「符号ミスでいつも答えが合わない…」「係数を揃えるのが面倒…」と苦手意識を持っている人もいるかもしれません。

この記事では、連立方程式の加減法を「手順」「注意点」「工夫」の3つの視点から徹底解説します。
さらに、レベル別の豊富な演習問題を通じて、あなたの習熟度に合わせて確実にスキルアップできるよう構成しました。

単に解き方を覚えるだけでなく、「どうすればミスなく、素早く解けるか」を自分で試行錯誤するヒントも紹介します。

この記事を最後まで読み終えるころには、連立方程式の加減法を自在に使いこなし、自信を持ってテストに臨めるようになっているはずです。

連立方程式の加減法の手順と注意点（前提知識）

連立方程式の加減法は、次の順で考えます。

最初に係数をそろえるとき、どちらの文字をそろえてもいいです。

ただ、計算を工夫する余地はたくさんあります。
たとえば、次のような工夫が考えられます。

• できるだけ数字が大きくならないようにすると、スムーズに計算しやすいです。
• 足し算が計算しやすい
  ⇒異符号の文字を消去する
  引き算が計算しやすい
  ⇒同符号の文字を消去する
• 先頭の項の消去があまり好きではない
  ⇒2番目の項から消去する

どれも厳密なルールではないので、
自分なりに計算しやすい方法を見つけてください。

加減法で起こしやすいミス

加減法のミスのほとんどは、この2つのどちらかです。
計算するときは、必ず注意して計算するようにしましょう。

連立方程式の加減法を例題で理解

【解説】

• \(b\)から消去する
  ⇒\(b\)の係数をそろえる
  ⇒式①の両辺に2、式②の両辺に3をかける
• 係数が異符号
  ⇒2式を足し算する

\(4a+6b=-2\)…①’（①×2）
\(9a-6b=15\)…②’（②×3)

①’＋②’のひっ算をすると

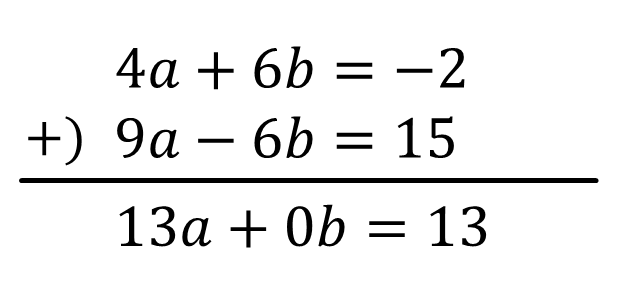
\(13a=13 \\ a = 1\)

①に\(a\)の値を代入して
\(2+3b=-1 \\ 3b=-3 \\ b = -1\)

連立方程式の検算（代入法の演習記事でも同じことを書いています）

連立方程式では、最後に代入した式と違う方の式に（例題では式②）に代入すると、答えが正しいかどうかを確認できます。
代入しても等式が成立すれば、それが正しい答えであるとわかります。

実際に、例題で\(a=1,b=-1\)を式②に代入すると
\(2 \times 1 -3 \times(-1) =5\)

となり式②が成り立つので、
\(a=1,b=-1\)が正しい答えであると確認できます。

レベル別の演習問題で加減法をマスター！

足し算、引き算のひっ算に慣れよう

解説

• \(x\)の係数の数字がそろっている
  ⇒\(x\)から消去する
• 係数が異符号
  ⇒2式を足し算する

①＋②のひっ算をすると

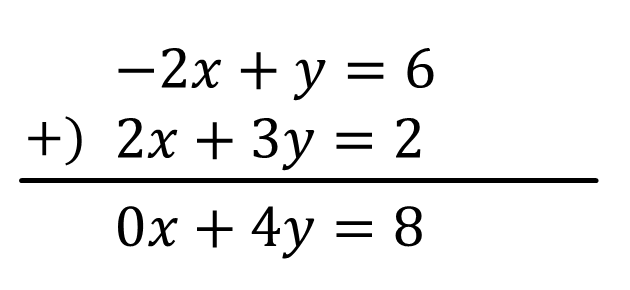
\(4y=8 \\ y=2\)

①に\(y\)の値を代入して
\(-2x+2=6 \\ -2x=4 \\ x=-2\)

よって\(x=-2,y=2\)

---

解説

• \(b\)の係数の数字がそろっている
  ⇒\(b\)から消去する
• 係数が同符号
  ⇒2式を引き算する

①－②のひっ算をすると

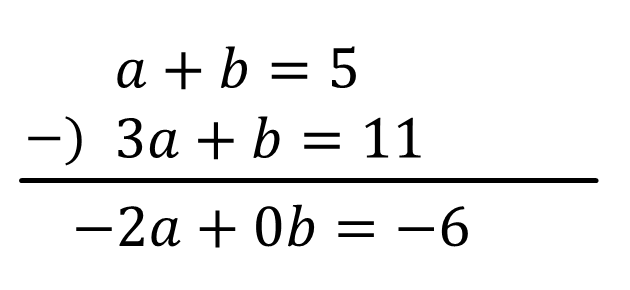
\(-2a=-6 \\ a=3\)

①に\(a\)の値を代入して
\(3+b=5 \\ b=2\)

よって\(a=3,b=2\)

一次関数の式を求めるときは、こういう\(b\)がそろった連立方程式を解いて求めます。

係数をそろえる操作に慣れよう

解説

②式の\(y\)の係数が1
⇒\(y\)の係数をそろえる
⇒②の両辺に2をかける

\(5x+2y=3\)…①
\(6x-2y=8\)…②’（②×2）

①＋②’のひっ算をすると

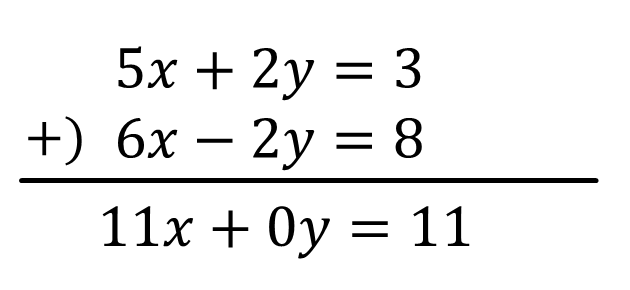
\(11x=11 \\ x=1\)

①に\(x\)の値を代入して
\(5+2y=3 \\ 2y=-2 \\ y=-1\)

よって\(x=1,y=-1\)

係数が1の文字があるときは、そちらから消去するとはやいです。

---

解説

• ②式の\(b\)の係数が1
  ⇒\(b\)の係数をそろえる
  ⇒②式の両辺に3をかける

\(5a+3b=-4\)…①
\(-6a+3b=-15\)…②’（②×3）

①－②’のひっ算をすると

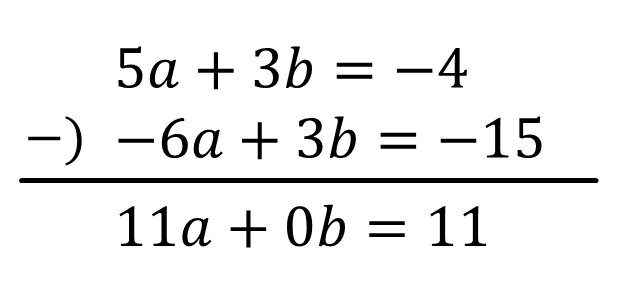
\(11a=11 \\ a=1\)

①に\(a\)の値を代入して
\(5+3b=-4 \\ 3b=-9 \\ b=-3\)

よって\(a=1,b=-3\)

この計算の、\(a\)の項や、定数項のように、負の数をひき算をするときに計算ミスが起こりやすいです。

係数をそろえる操作をマスターしよう

解説

• \(x,y\)のどちらでそろえてもよいが、係数が小さいものでそろえる方が計算しやすいことが多い
  ⇒(x\)の係数をそろえる
  ⇒①の両辺に3、②の両辺に2をかける

\(6x+15y=-24\)…①’（①×3）
\(6x+4y=-2\)…②’（②×2)

①－②’のひっ算をすると

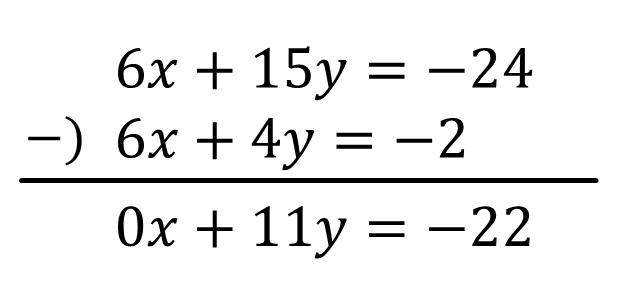
\(11y=-22 \\ y=-2\)

①に\(x\)の値を代入して
\(2x-10=-8 \\ 2x=2 \\ x=1\)

よって\(x=1,y=-2\)

一方の文字を求めた後、もうひとつの文字を求めるために代入するときは、変形前の①か②に代入した方がよいです。
①’、②’に変形するときの計算で間違っている可能性もあるからです。
答えを最後まで求めたあとに、元の式の①か②で検算すれば、変形中のミスも見つけることができます。

---

解説

• \(b\)をそろえる
  ⇒式①の両辺に2、式②の両辺に5をかける

\(12a+10b=-14\)…①'(①×2)
\(25a－10b=-60\)…②’（②×5）

①’＋②’のひっ算をすると

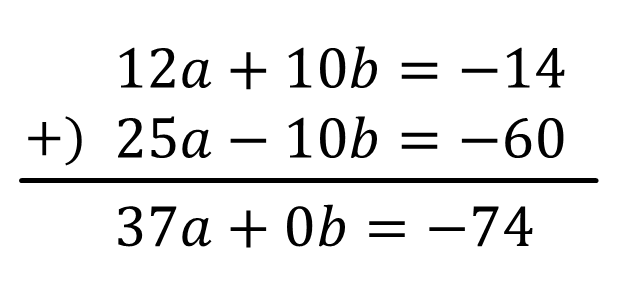
\(37a=-74 \\ a=-2\)

①に\(a\)の値を代入して
\(-12+5b=-7 \\ 5b=5 \\ b=1\)

よって\(a=-2,b=1\)

この計算の、\(a\)の項や、定数項のように、負の数をひき算をするときに計算ミスが起こりやすいです。

分数係数の問題で、加減法を自由自在に！

解説

分数は考えにくいので、両辺に同じ数をかけて分母をはらう
⇒式①の両辺に2をかける

\(x+2y=4\)…①’（①×2）
\(2x+3y=7\)…②

①’の式の\(x\)の係数が1
⇒\(x\)をそろえる
⇒式①の両辺に2をかける

\(2x+4y=8\)…①”（①’×2）
\(2x+3y=7\)…②

①”－②のひっ算をすると

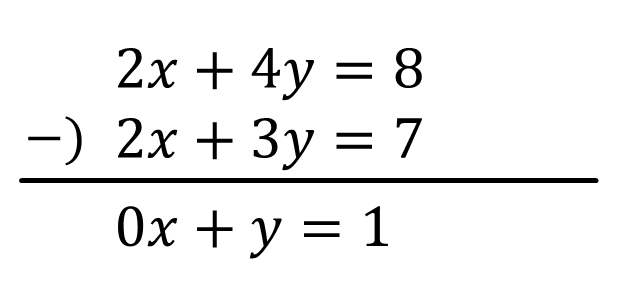
\(y=1\)

②に\(y\)の値を代入して
\(2x+3=7 \\ 2x=4 \\ x=2\)

よって\(x=2,y=1\)

---

解説

②式の分数をはらう
⇒②式の両辺に6をかける

\(2a+3b=13\)…①
\(3a+2b=12\)…②’（②×6）

\(b\)の係数をそろえる
⇒①の両辺に2、②’の両辺に3をかける

4a+6b=26…①’（①×2）
9a+6b=36…②”（②’×3）

①’－②”のひっ算をすると

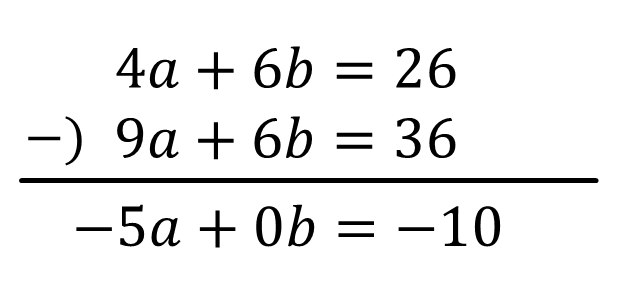
\(-5a=-10 \\ a=2\)

①に\(a\)の値を代入して
\(4+3b=13 \\ 3b=9 \\ b=3\)

よって\(a=2,b=3\)

両辺へのかけ算をするタイミングが3回もあります。
それだけかけ忘れやすくなるので、注意してください。

おわりに

この記事では、連立方程式の加減法について、基本手順から、ミスしやすいポイント、そして分数係数を含む応用問題まで、幅広く解説しました。

重要なのは、「これが正解」と決められた解き方に固執せず、自分にとって最も計算しやすい方法を見つけることです。
特に、係数を揃える操作や、足し算・引き算の符号の扱いは、慣れが求められます。

レベル別演習でたくさん手を動かし、ご紹介した工夫や検算方法を試しながら、加減法をあなたの強力な武器にしてください。

連立方程式には、今回扱った「加減法」の他に「代入法」という解き方もあります。
それぞれの特徴を理解し、問題に合わせて使い分けられるようになると、連立方程式のマスターは完了です。

次のステップとして、代入法についても演習してみましょう。

← 一つ前のページに戻る

← 一つ前のページに戻る