突然ですが、あなたは連立方程式の解き方をスラスラと思い浮かべられますか？
中学生の数学でつまずきやすいこの分野は、これから学ぶ**「関数」や「図形」の問題を解くための非常に重要な土台となります。特に、このブログのテーマである関数**をマスターするには、連立方程式を解く力が不可欠です。
この記事では、連立方程式の基本的な考え方から、加減法と代入法の2つの解き方を、具体例を通して徹底解説します。さらに、計算ミスを防ぐための注意点や、代入法を苦手にしないための最大のコツまで伝授します。
「連立方程式は苦手だ…」と感じているあなたも大丈夫です。この記事を読んで、どんな問題にも自信を持って取り組めるスキルを一緒に身につけていきましょう！
連立方程式って何？
中学校では、「文字が2種類ある式が2本」の連立方程式の解き方について学びます。
ここからは、それに準じて説明していきます。
具体例でイメージをつかもう
次のような2式を考えてみます。
\(x+y=2\)…①
\(x-y=0\)…②
たとえば、①の式 \(x+y=2\)を満たす\(x,y\)の組は、
\((0,2),(1,1),(2,0),(3,-1)…\)のように無数に存在します。
同じように、②の式\(x-y=0\)を満たすす\(x,y\)の組も、
\((0,0),(1,1),(2,2),(3,3)…\) のように無数に存在します。
これらの無数にある解の中で、\((x,y)=(1,1)\)のように、両方の式に共通する解が存在します。
このような、複数の式に共通する解を求めたいときに、用いるのが連立方程式なのです。
なぜ解法が必要なの？
先ほどの例のように、書き出してすぐ見つかることはほとんどありません。
実際には、式が複雑だったり、解が分数や大きな数字になったりして、「適当に考えて」答えを見つけるのは非常に困難です。
そのため、どんな連立方程式でも、確実に、素早く解を導き出せるように、加減法と代入法という2つの解き方について学びます。
次の章では、これらの方法を説明していきます。
しっかりマスターし、どんな連立方程式も解けるスキルを身につけていきましょう！
加減法ってどういう解き方？
加減法では、次の手順で計算します。
連立方程式の加減法を具体例で確認
次のような連立方程式を例に考えてみましょう。
\(2a+3b=5\)…①
\(3a-2b=1\)…②
どちらかの文字の係数をそろえる
今回は、\(a\)の係数（2と3)を、最小公倍数の6にそろえることにします。
「両辺に同じ数をかけても等号は成立する」
という等式の性質を利用して、
式①の両辺に3、式②の両辺に2をかけると、
式は次のように変形できます。
\(6a+9b=15\)…①’
\(6a-4b=2\)…②’
これで、\(a\)の係数がそろいました。
ひっ算でそろえた文字を消す
\(a\)の係数がそろったら、①’から②’を引き算し、\(a\)を消去します。
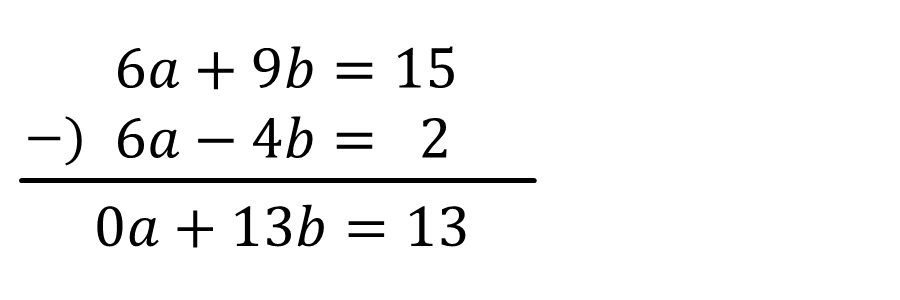
\(a\)の項、\(b\)の項、定数項同士、それぞれで引き算しています。
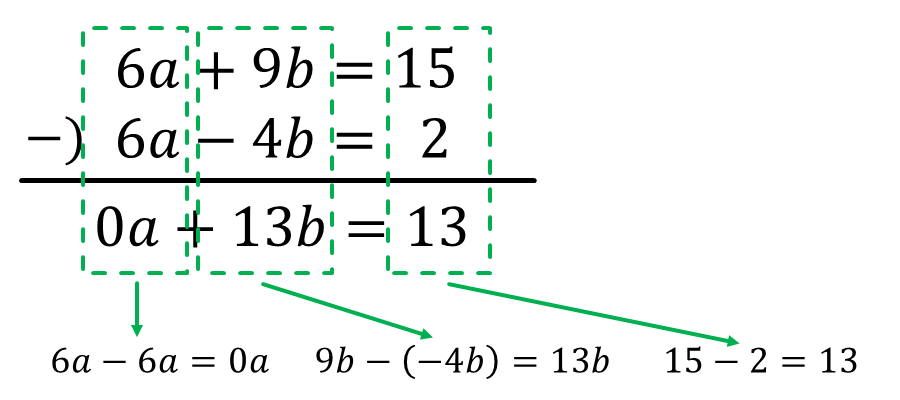
【ポイント】
消したい文字が同符号のときは引き算（今回）、
異符号のときは足し算をします。
これを計算すると、
\(13b = 13\\ b = 1\)
と\(b\)を求めることができました。
求めた値を代入して、最初に消去した文字の値を求める
求めた\(b=1\)を、元の式①または②のシンプルな方に代入して、\(a\)の値を求めます。
（今回は①に代入します）
\(2a+3b=5 \\ 2a+3 \times(1)=5 \\ 2a+3=5 \\ 2a=2 \\ a=1\)
これで\(a=1,b=1\)と答えを求めることができました。
連立方程式の加減法で気を付けるべきミス
ぼくの経験上ですが、ミスのほとんどはこの2つです。
文章題などを解いていて、分数になるはずのないところで分数が答えになったときは、
真っ先にこの2つを確認するとよいです。
特に符号ミスは、係数がマイナスの項（例\(-4b\)）を引き算するときに起こしやすいので、
注意して計算してください。
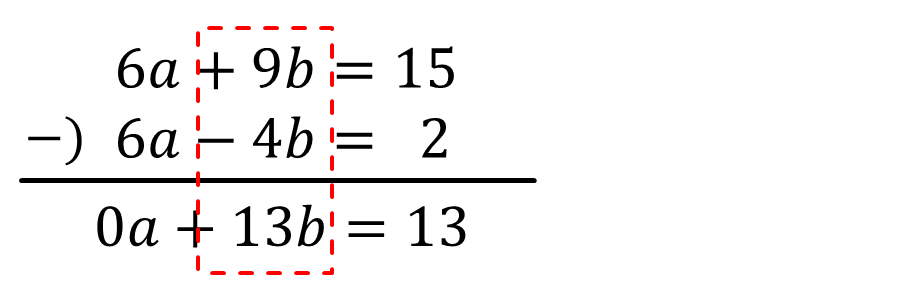
代入法ってどういう解き方？
代入法では、次の手順で計算します。
連立方程式の代入法を具体例で確認
次のような連立方程式を例に考えてみましょう。
\(2x-2y=1\)…①
\(\displaystyle -\frac{1}{2}x+y=2\)…②
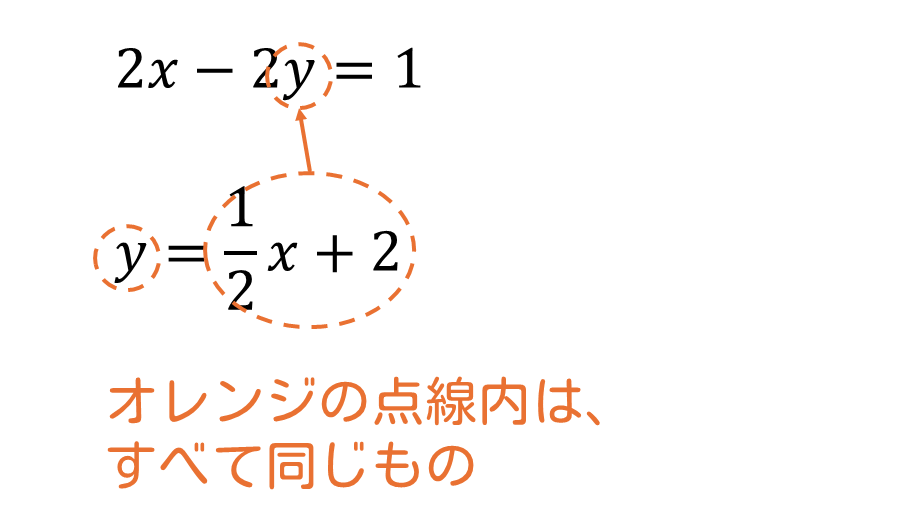
どちらかの式を「(文字)=○」の形に変形する
式②の\(y\)の係数が1であるため、②を「\(y=◯\)」に変形します。
\(\displaystyle -\frac{1}{2}x+y=2\)
\(\displaystyle y =\frac{1}{2}x+2\)…②’
変形した式を、もう一方の式に代入して計算する
変形した式をもう一方の式に代入します。
（今回は②’を①に代入）
①式の\(y\)の部分を、②式の右辺と入れ替えたと考えるとわかりやすいと思います。
\(\displaystyle 2x-2(\frac{1}{2}x+2)=1 \\ 2x-x-4 = 1 \\ x = 5\)
求めた値を代入して、もう一方の文字の値を求める
求めた値を方程式に代入して、もう一方の文字の値を求めます。
代入法の場合は、変形した式に代入すると、移項などの手間がなく計算することができます。
②’の式に、求めた\(x\)の値を代入すると
\(\displaystyle y =\frac{1}{2}x+2 \\ \displaystyle y = \frac{1}{2} \times(5) +2 \\ \displaystyle y = \frac{5}{2} +2 \\ \displaystyle y = \frac{9}{2} \)
代入法をマスターする最大のコツ：式を「ひとかたまり」で見る
代入法を考えるコツは、「(文字)=○」の式の右辺をひとかたまりと見ることです。
たとえば、\(y=2x-1\)という式があるとき、\(y\)と\(2x-1\)を完全に等しい「ブロック」だと見なす意識が大切です。
代入法は、このブロックを組み替えていると思ってください。
加減法と代入法、加減法に頼りすぎることの危険性について
中学生の連立方程式では、加減法だけでなく代入法もしっかり身につけておくべきです。
ただ、代入法を苦手に感じる生徒はとても多いです。
だいたいが、次のような理由があります。
- 授業では加減法を先に習う
⇒「連立方程式＝加減法で解くもの」という意識が強くなりがち - 加減法だけでもすべての連立方程式は解ける
⇒「代入法は別に使えなくてもいいのでは？」と思ってしまいがち - 代入法は「式をひとかたまりとして扱う」感覚が必要
⇒の感覚がないと、どうしても理解しづらくなる
とはいえ、代入法は学習しておいた方が確実にメリットがあります。
- 問題によっては代入法の方が圧倒的に簡単に解ける
⇒特にどちらかの式が「\(x=〜\)」や「\(y=～\)」の形に近い場合など - 数学の学習が進むにつれて、式をひとかたまりとして見る場面はどんどん増える
⇒代入法はそのための大事なトレーニング
単に「2つの解き方を覚える」というだけでなく、今後の数学の土台をつくるつもりで、代入法にもぜひ取り組んでみてください。
おわりに
お疲れ様でした！連立方程式の加減法と代入法について、マスターするための手順とコツを学ぶことができました。
連立方程式の解法とは、複雑な「文字が2つある式」を「文字が1つだけの式」に変形する、
「問題をシンプルにするツール」です。
- 加減法：係数を揃えて、文字を消去する。
- 代入法：「ひとかたまり」で見て、文字を置き換えて消去する。
特に、代入法で身につけた「式をひとかたまりで見る」感覚は、今後の関数（グラフの交点など）を解く上で非常に重要です。
加減法だけでなく代入法にも積極的に取り組み、あなたの数学の土台を強固なものにしていきましょう！
コメント