「関数の計算、理屈はわかるけど実際に解こうとすると手が止まってしまう…」
そんな悩みはありませんか?
一次関数の問題で、座標を求める作業は「空気」のように当たり前に使う基本スキルです。
ここでもたつくと、応用問題で時間が足りなくなってしまいます。
この記事では、基本的な代入の方法から、少しややこしい分数の計算まで、ステップアップ形式で演習を用意しました。
「代入して解く」という感覚を、この演習を通して体に染み込ませていきましょう!
【関連記事】
- 一次関数のグラフ上の点の求め方について自信がない方はこちら
一次関数のグラフ上の点は、グラフの式に\(x\)または\(y\)を代入すると求めることができます。
グラフ上の点の求め方や、基本になる考え方について、くわしく解説しています。
こちらもぜひお読みください。
👉一次関数のグラフ上の点の求め方を超シンプル解説!
一次関数のグラフ上の点の求め方(前提知識)
グラフ上の点の求め方は、基本知識としてそのまま問われることも、応用問題の前処理として使うこともあります。
関数が範囲のテストで、この計算をしないということは絶対にない、超重要事項です。
軸上の点の考え方
\(x\)座標は、\(y\)軸からの距離を表します。
そのため、\(y\)軸上の点は\(x\)座標が0です。
また、\(y\)座標は、\(x\)軸からの距離を表します。
そのため、\(x\)軸上の点は\(y\)座標が0です。
どちらも、意味を理解せずに覚えていると、急に出てくるとわからなくなるので、
しっかり意味を理解しておいてください。

ここからは、この前提知識をつかって問題を解いていきます。
例題
例題
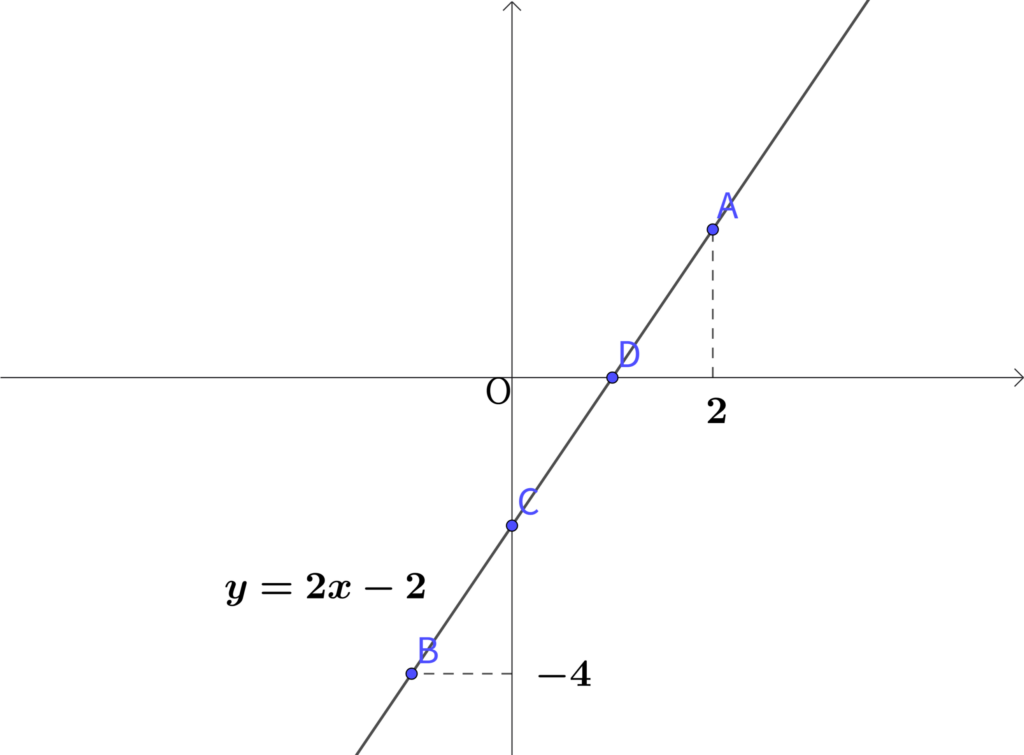
次の図は、直線\(y=2x-2\)のグラフである。
次の問に答えなさい。
1)
\(x\)座標が\(2\)である点Aの座標を求めなさい。
2)
\(y\)座標が\(-4\)である点Bの座標を求めなさい。
3)
\(y\)軸上の点である点Cの座標を求めなさい。
4)
\(x\)軸上の点である点Dの座標を求めなさい。
【解説】
1)
\(y\)座標は、グラフの式に\(x\)座標を代入して求める。
\(y=2x-2\)に\(x=2\)を代入すると
\(y=2 \times 2-2 =2\)
よって点A\((2,2)\)
2)
\(x\)座標は、グラフの式に\(x\)座標を代入して求める。
\(y=2x-2\)に\(y=-4\)を代入すると
\(-4=2x-2 \\ 2x =-4+2 \\2x = -2 \\ x=-1\)
よって点B\((-1,-4)\)
3)
\(y\)軸上の点の\(x\)座標は\(0\)
\(y=2x-2\)に\(x=0\)を代入すると
\(y=-2\)
よって点C\((0,-2)\)

ちなみに、\(y\)軸上の点は切片のことです。
切片の意味がきちんとわかっていたら、
計算せずに最初から答えだけ書いても大丈夫です。
ただ、他の関数では切片ほどわかりやすくなかったりするので、
「\(y\)軸上の点の\(x\)座標は\(0\)」ということは、必ず理解しておいてください。
4)
\(x\)軸上の点の\(y\)座標は\(0\)
\(y=2x-2\)に\(y=0\)を代入すると
\(0=2x-2 \\ 2x =2 \\ x=1\)
よって点D\((1,0)\)

\(x\)軸上の点の読み取りを忘れてしまう人を結構見かけます。
意味をちゃんと押さえて、忘れないようにしましょう。
演習
演習1(係数、定数項が整数の問題)
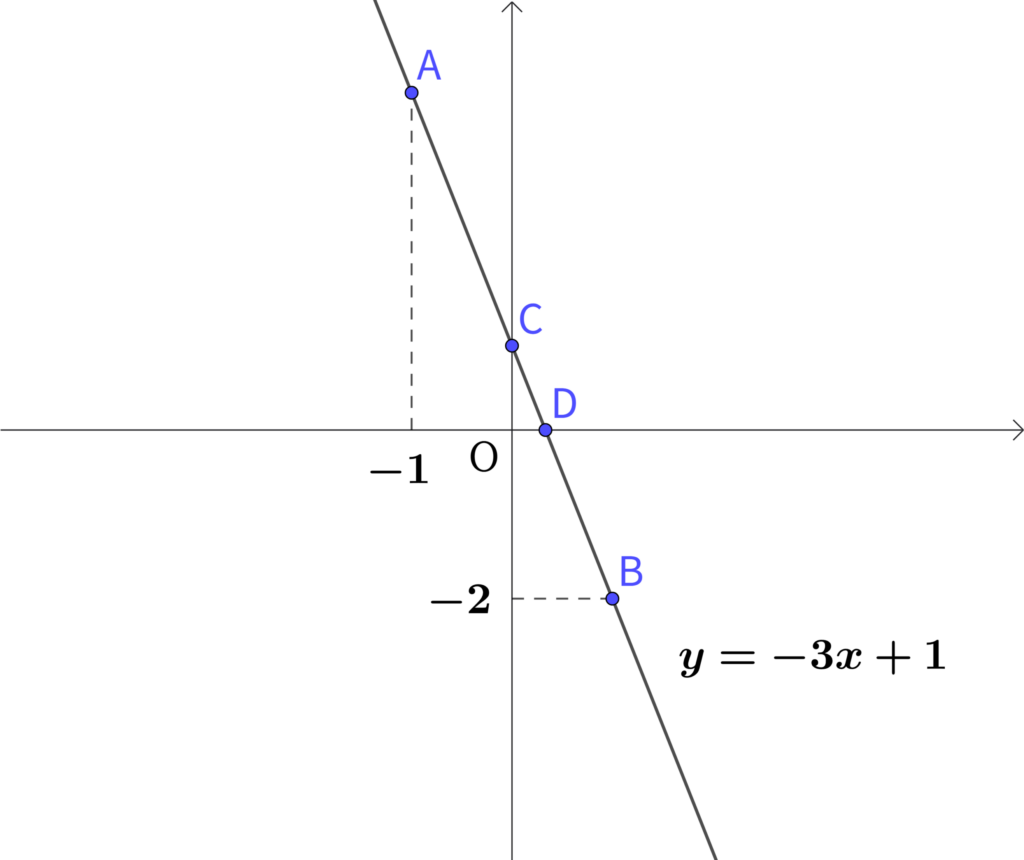
次の図は、直線\(y=-3x+1\)のグラフである。
次の問に答えなさい。
1)
\(x\)座標が\(-1\)である点Aの座標を求めなさい。
2)
\(y\)座標が\(-2\)である点Bの座標を求めなさい。
3)
\(y\)軸上の点である点Cの座標を求めなさい。
4)
\(x\)軸上の点である点Dの座標を求めなさい。
解説
1)
\(y=-3x+1\)に\(x=-1\)を代入すると
\(y=-3 \times (-1)+1 \\y =4\)
よって点A\((-1,4)\)
2)
\(y=-3x+1\)に\(y=-2\)を代入すると
\(-2=-3x+1 \\ 3x =1+2 \\3x = 3 \\ x=1\)
よって点B\((1,-2)\)
3)
\(y=-3x+1\)に\(x=0\)を代入すると
\(y=1\)
よって点C\((0,1)\)
4)
\(y=-3x+1\)に\(y=0\)を代入すると
\(0=-3x+1 \\ 3x =1 \\ \displaystyle x= \frac{1}{3}\)
よって点D\(\displaystyle (\frac{1}{3},0)\)
演習2(係数が分数、定数項が整数の問題)
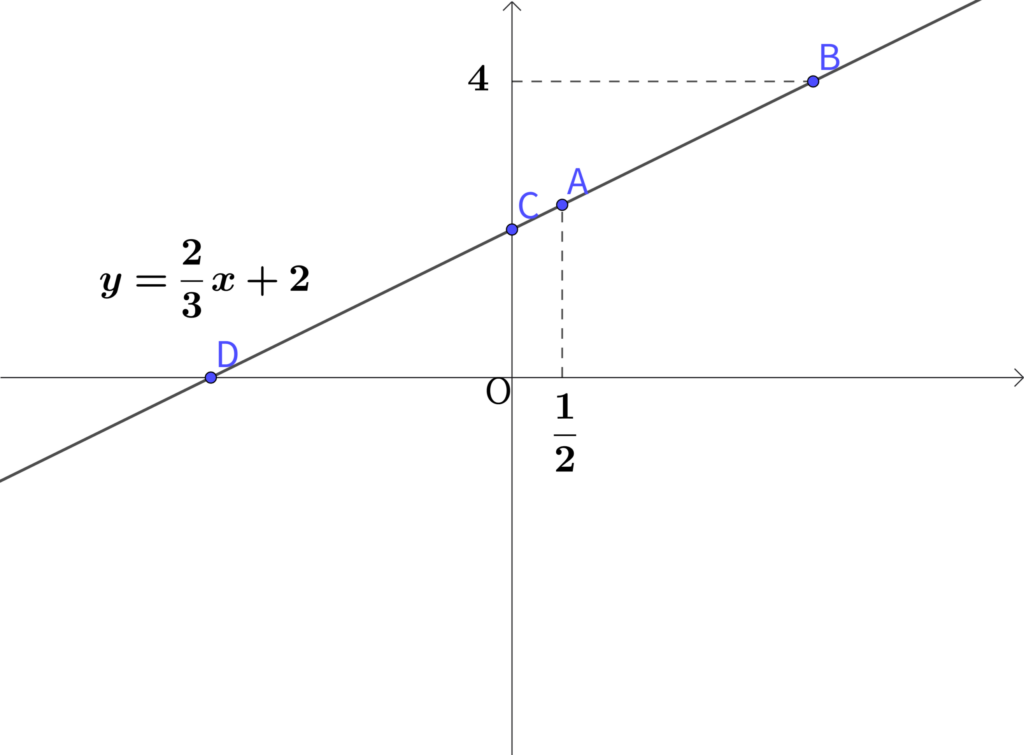
次の図は、直線\(\displaystyle y=\frac{2}{3}x+2\)のグラフである。
次の問に答えなさい。
1)
\(x\)座標が\(\displaystyle \frac{1}{2}\)である点Aの座標を求めなさい。
2)
\(y\)座標が\(4\)である点Bの座標を求めなさい。
3)
\(y\)軸上の点である点Cの座標を求めなさい。
4)
\(x\)軸上の点である点Dの座標を求めなさい。
解説
1)
\(\displaystyle y=\frac{2}{3}x+2\)に\(\displaystyle x=\frac{1}{2}\)を代入すると
\(\displaystyle y=\frac{2}{3} \times \frac{1}{2}+2 \\ y = \displaystyle \frac{1}{3}+\frac{6}{3}\\ \displaystyle y=\frac{7}{3}\)
よって点A\(\displaystyle (\frac{1}{2},\frac{7}{3})\)
2)
\(\displaystyle y=\frac{2}{3}x+2\)に\(y=4\)を代入すると
\(\displaystyle 4=\frac{2}{3}x+2 \\ \displaystyle \frac{2}{3}x = 2 \\ x=3\)
よって点B\((3,4)\)
3)
\(\displaystyle y=\frac{2}{3}x+2\)に\(x=0\)を代入すると
\(y=2\)
よって点C\((0,2)\)
4)
\(\displaystyle y=\frac{2}{3}x+2\)に\(y=0\)を代入すると
\(\displaystyle 0=\frac{2}{3}x+2 \\ \displaystyle \frac{2}{3}x=-2 \\ x=-3\)
よって点D\(\displaystyle (-3,0)\)
演習3(係数、定数項が分数の問題)
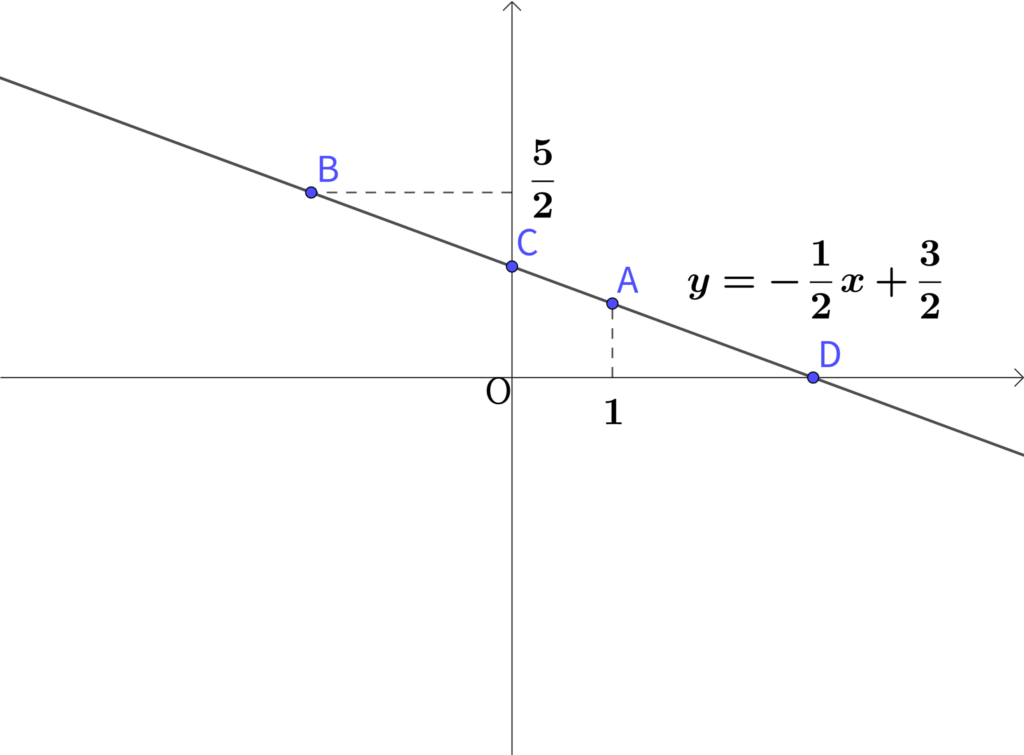
次の図は、直線\(\displaystyle y=-\frac{1}{2}x+\frac{2}{3}\)のグラフである。
次の問に答えなさい。
1)
\(x\)座標が\(1\)である点Aの座標を求めなさい。
2)
\(y\)座標が\(\displaystyle \frac{5}{2}\)である点Bの座標を求めなさい。
3)
\(y\)軸上の点である点Cの座標を求めなさい。
4)
\(x\)軸上の点である点Dの座標を求めなさい。
解説
1)
\(\displaystyle y=-\frac{1}{2}x+\frac{3}{2}\)に\(\displaystyle x=1\)を代入すると
\(\displaystyle y=-\frac{1}{2} \times 1 +\frac{3}{2} \\ y = \displaystyle \frac{2}{2}\\ \displaystyle y=1\)
よって点A\(\displaystyle (1,1)\)
2)
\(\displaystyle y=-\frac{1}{2}x+\frac{3}{2}\)に\(\displaystyle y= \frac{5}{2}\)を代入すると
\(\displaystyle \frac{5}{2}=-\frac{1}{2}x+\frac{3}{2} \\ \displaystyle \frac{1}{2}x = \frac{3}{2}-\frac{5}{2} \\ \displaystyle \frac{1}{2}x=-1 \\ x=-2\)
よって点B\(\displaystyle (-2,\frac{5}{2})\)
3)
\(\displaystyle y=-\frac{1}{2}x+\frac{3}{2}\)に\(x=0\)を代入すると
\(\displaystyle y=\frac{3}{2}\)
よって点C\(\displaystyle (0,\frac{3}{2})\)
4)
\(\displaystyle y=-\frac{1}{2}x+\frac{3}{2}\)に\(y=0\)を代入すると
\(\displaystyle 0=-\frac{1}{2}x+\frac{3}{2} \\ \displaystyle \frac{1}{2}x=\frac{3}{2} \\ x=3\)
よって点D\(\displaystyle (3,0)\)
おわりに
お疲れ様でした!最後まで解ききれたでしょうか?
グラフ上の点の求め方のポイントはたった2つです。
- \(x\)座標がわかれば\(y\)を、\(y\)座標がわかれば\(x\)を代入
- 「軸上の点」の\(x\)座標または\(y\)座標を読めるようにする
最初は分数の計算でミスをすることもあるかもしれませんが、何度も繰り返すうちに必ずスピードも精度も上がります。
この「点の求め方」ができるようになると、次はや「図形の面積」といった、テストで高得点を狙える応用問題にも挑戦できるようになります。
自信がついた方は、ぜひ次のステップの演習にもチャレンジしてみてくださいね!
【関連記事】
- 一次関数のグラフ上の点の求め方について理解を深めたい方はこちら
今回演習した一次関数のグラフ上の点の求め方。
考え方をしっかり押さえておくと、応用問題で考えを整理しやすくなります。
グラフ上の点の求め方や、基本になる考え方について、くわしく解説しているので、ぜひ読んでみてください。
👉一次関数のグラフ上の点の求め方を超シンプル解説! - 一次関数のまとめに戻る方はこちら
関数は、抽象的で取り組みづらい反面、同じ操作が繰り返し出てくるので、コツが掴めると得意にしやすい分野でもあります。
考え方からていねいに解説しているので、ぜひ先々まで活用できるかたちで知識を身に付けてください。
👉【完全攻略】一次関数の解き方・考え方を基礎からじっくり


コメント