「関数のグラフって、そもそも何だろう?」
そう聞かれると、意外とすぐには答えにくいかもしれません。
関数の式を満たすグラフは点の集まりです。
何となくグラフを描ける人でも、実は、この「グラフの意味」をしっかり理解していないことがよくあります。
でも、グラフの意味をしっかり理解しておくと、グラフ上の点の求め方、変域、グラフの交点など、グラフに関するいろいろなことの理解が深まります。
この記事では、比例のグラフを用いて、グラフの意味についてわかりやすく解説します。
関数のグラフとは?関数の式とグラフの関係
グラフの意味を比例の式で具体的に見てみよう
グラフは、関数の式を満たす点を座標にとっていったものです。
関数の式を満たす点が無数にあるため、線で代表して描いています。
言葉だけではどういうことかわかりづらいと思うので、実際の関数で考えてみます。
\(y=2x\)という比例の式を考えます。
この式で、\(x\)の値をいくつか決めて\(y\)の値を求めると、次のような表が作れます。
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
次に、この表の\(x\)と\(y\)を、グラフ用紙にとります。
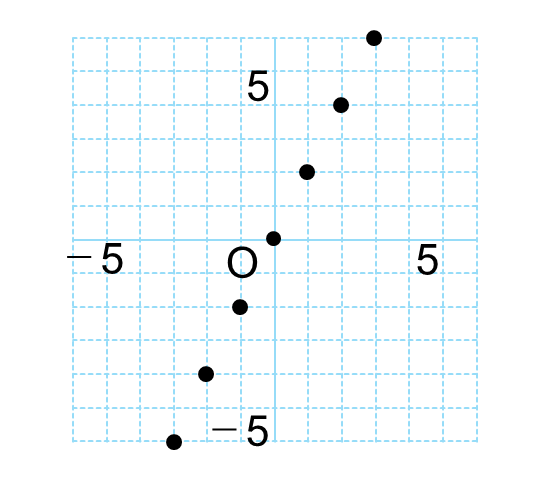
しかし、\(x\)の値は整数に限りません。
たとえば、\(x\)=0と\(x\)=1の間にも、無数の値が存在します。
また、この式では、\(x\)が1増えると\(y\)は2ずつ増えるという一定の割合で変化しています。
つまり、\(x\)の値を細かく変えていくと、無数の点をとることができます。
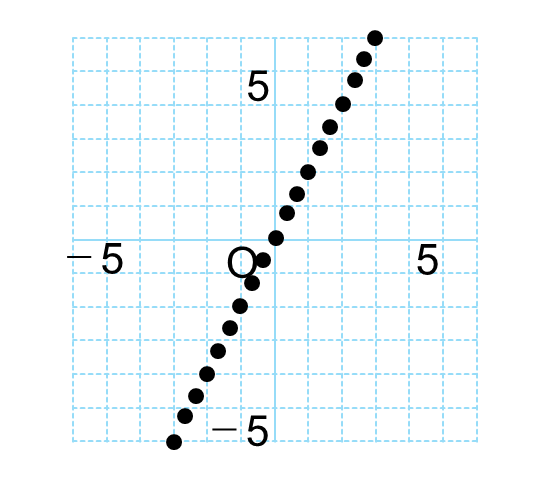
いちいち点を打つのは大変なので、それらの点を線で置き換えます。
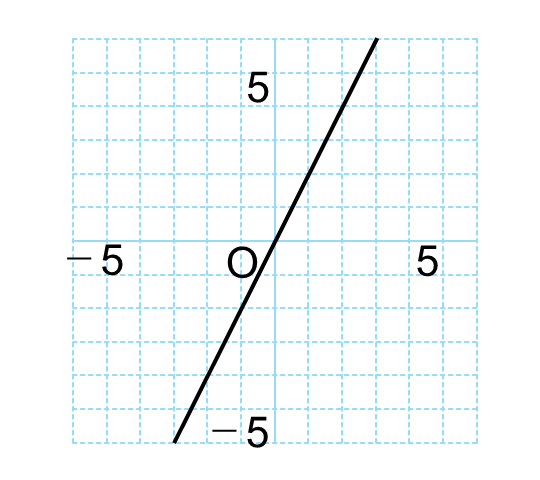
こうやってできた図を、関数のグラフと呼んでいます。
まとめると、関数の式を満たす\(x\)と\(y\)の組をいくつもとり、それらの点を線で結んだものがグラフです。
つまり、グラフは関数の式を満たす点の集まりということです。

比例のグラフで考えましたが、どんな関数のグラフも「式を満たす点の集まり」ということに変わりはありません。
グラフ上の点の計算方法
グラフ上の点の計算方法を具体例で見てみよう
グラフは関数の式を満たす点の集まりです。
だから、グラフ上の点を知りたいときは、関数の式に値を代入すればグラフ上の点を計算することができます。
たとえば、関数\(y=2x\)のグラフで
\(x=3\)のときの\(y\)座標は、
関数の式\(y=2x\)に\(x=3\)を代入して
\(y=2 \times 3 \\ y=6\)
と計算できます。
また、\(y=-4\)のときの\(x\)座標は、
関数の式\(y=2x\)に\(y=-4\)を代入して
\(-4=2x \\x =-2\)
と計算できます。

形が違うのでわかりづらいですが、関数の式で、\(x\)、\(y\)を計算するときと同じことをしています。
おわりに
今回の内容は、グラフの意味について解説しました。
グラフは関数の式を満たす点の集まり
あまりテストの点数に直結する話ではないですが、この意味がしっかり理解できると、グラフに関する話の見え方ががらっと変わります。
たとえば、
グラフ上の点を求めるときは、その関数の式を満たす点を1つ見つけていること。
交点を求めるときは、2つの式を同時に満たす点を探していること。
変域を考えるときは、\(x\)が動くときに点がどんな\(y\)の値をとるかを見ていること。
どの内容も「グラフは点の集まり」という考えでつながっています。
このことがわかると、関数のいろいろな単元が“ひとつの流れ”として見えてきます。
グラフを扱うときは、ぜひ「点の集まり」として意識してみてください。
まとめページへ




コメント