【定期テスト対策・中2数学】一次関数の変域｜確実に得点するグラフ活用テクニック

一次関数の問題でよく出てくる変域。
「\(x\)の値を式に入れて、\(y\)の範囲を出すだけでしょ？」と思っていませんか？

たしかに、定期テストではそれで正解が出せます。
でも、本当のところは、グラフ上で\(x\)と\(y\)がどう対応しているかを考える必要があり、
グラフの有効範囲を描いて、\(y\)の値を読み取って求めます。

今回の記事では、変域の問題の正しい解き方について、わかりやすく解説します。

一次関数の変域ってどう求めたらいいの？

【4ステップ】一次関数の変域の求め方

変域の問題は、有効な範囲のグラフを描き、そのグラフの最も低い\(y\)座標と最も高い\(y\)座標を読み取るのが基本的な解法の流れです。

そして、次の4ステップで考えると、有効な部分が整理しやすくなります。

一次関数の変域の解き方を詳しく解説

\(\displaystyle y= -\frac{3}{4}x+1\)

この関数で、
\(x\)の変域が\(-1≦x≦2\)のときの
\(y\)のの変域を求めてみます。

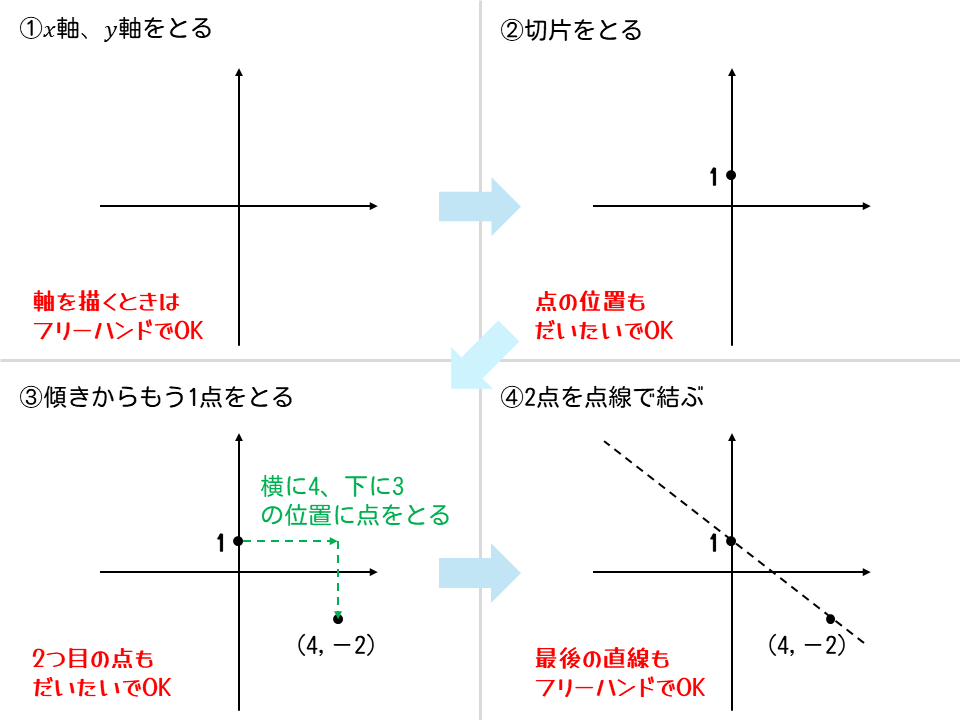
【全体像】変域がないものとして、関数のグラフ全体を点線で描く

まず、次の手順で簡略なグラフを描きます。
（全部フリーハンドでOKです）

1. \(x\)軸、\(y\)軸をとる
2. 切片をとる
3. 傾きからもう1点をとる
4. 2点を点線で結ぶ

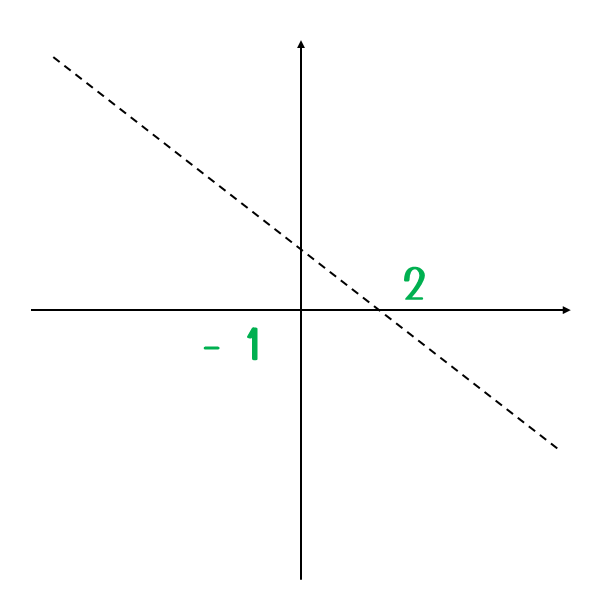
【条件設定】\(x\)の変域を\(x\)軸上に書き込む

\(x\)の変域を\(x\)軸上に書き込みます。
この範囲外の\(x\)座標は、今回有効ではありません。

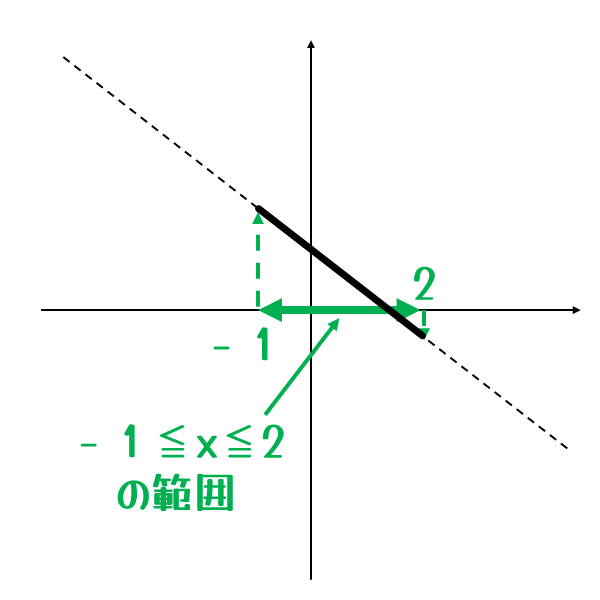
【絞り込み】グラフの\(x\)の変域内にある部分だけを実線でなぞる

グラフで、\(x\)座標が変域内にある部分だけを実線でなぞります。
これで、グラフのどの部分が有効なのかが一目でわかります。

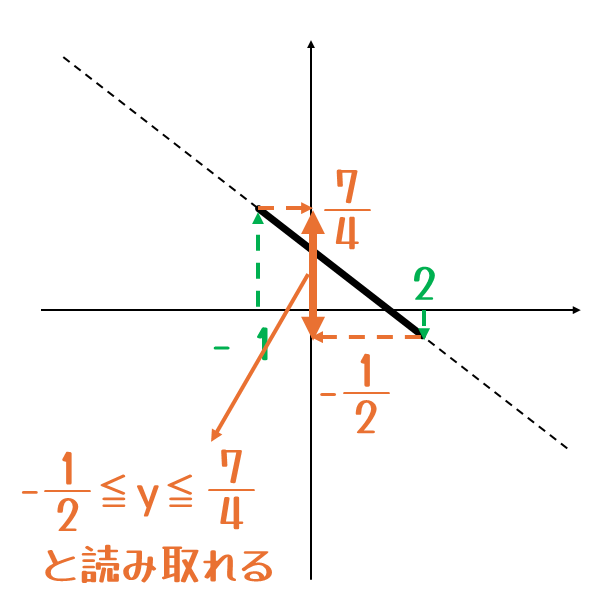
【答え】グラフの実線部の\(y\)座標の下端から上端までを読み取る

一次関数の式に、\(x\)の変域の端の点を代入して、そのときの\(y\)を計算し、それをグラフに書き入れます。

• \(x=-1\)のとき
  \(\displaystyle y= -\frac{3}{4} \times (-1)+1=\frac{7}{4}\)
• \(x=2\)のとき
  \(\displaystyle y= -\frac{3}{4} \times 2+1=-\frac{1}{2}\)

これで、図から\(y\)のとり得る値の範囲、つまり変域が

\( \displaystyle -\frac{1}{2}≦y≦\frac{7}{4}\)

であるとわかります。

変域を考えるためには

• 座標の読み方
• グラフの描き方
• 点の集まりとしてのグラフのイメージ
• グラフ上の点の求め方

などの複合的な力が求められます。
それぞれ、ページの最後にリンクを用意していますので、自分に足りないと思うものは、ぜひ読んでみてください。

何で変域の端を代入するだけの解法はおすすめじゃないの？

一次関数の変域を出したいだけなら、実は、グラフを描かなくても次の手順で変域を出すことはできます。

1. \(x\)の変域の端の\(y\)座標を求める
2. 不等式が成り立つように、\(y\)の値を当てはめる

ただ、この解き方、よく見かけますがまったくおすすめしません。
理由は、一次関数でしか通用しない解き方だからです。

この解き方が成立するのは、次の2つの条件がそろっているからです。

• 一次関数は、\(x\)が増えるとずっと増えるか、ずっと減るかの関数
• 出題される\(x\)の変域が「\(◯≦x≦△\)」のような閉じた変域

逆に言えば、この2つが成立しないと、冒頭でお示しした解き方は使えません。
そして、中3の二次関数では、この2つが成立しなくなります。

そのため、中2の二次関数を簡略化した手順で覚えていると、
中3の二次関数の変域用の解き方を、また別で覚えなくてはならなくなってしまいます。
高校受験で変域の解き方を忘れる人がよくいますが、大半は、定期テストのときにそれぞれ別の解法として覚えたからです。

さらに言うと、高校の複雑な関数になると、単純な解き方に集約することは難しくなります。

だから、結局は「グラフの有効域を描く⇒変域を読み取る」という、本質的な解き方が、最終的には一番の近道になります。

おわりに

今回は、一次関数の変域の求め方についての記事でした。

一次関数の変域は、

1. グラフの有効域を描く
2. \(y\)座標を読み取る

の順で考えれば必ず求めることができます。
そして、これは一次関数以外のどんな関数であっても通用する解き方です。

確かに、一次関数に限っては端の点を代入して、不等号の帳尻を合わせれば正答は導けます。
でも、それは先の学習にはほとんど役に立たない、遠回りな解き方だということをわかっておいてください。

何度もグラフを描いて考えていくと、手順も定着すると思います。
がんばってください。

← 一つ前のページに戻る