「一次関数のグラフから式が読めない」
「一次関数のグラフのどこを見ればいいかわからない」
そんな経験ないですか?
関数のグラフは、式を視覚的に見やすくしたもので、式とは密接な関係にあります。
そのため、一次関数のグラフを読み取るときは、グラフを描くときと同じで「切片⇒傾き」の順に考えれば大丈夫です。
この記事では、一次関数のグラフから関数の式を読み取る方法についてわかりやすく解説しています。
【関連記事】
- グラフの基本的な描き方に自信がない方はこちら
「切片⇒傾き」の順でのグラフの描き方について解説しています。
グラフから式の読み取りは、式からグラフを描く方法の逆の操作なので、まずグラフの描き方を固めると、式の読み取りもスムーズに理解できます。
👉【3ステップ】「切片⇒傾き」で考える一次関数のグラフの描き方 - \(a,b\)のグラフ上での役割がわかりにくい方はこちら
傾き、切片の一次関数のグラフでの役割についてまとめました。
グラフの読み取りでも必要な知識なので、自信がない方は先にお読みください。
👉一次関数、グラフの描き方の基礎!傾き・切片のグラフ上での役割
一次関数のグラフから式を読み取るにはどうしたらいい?
一次関数のグラフは、「切片⇒傾き」の順で読む
一次関数のグラフの読み方をくわしく
まず、\(y\)軸を通る高さ(切片\(b\))はすぐにわかるので、ここを最初に読み取ります。
次に、切片から右に動いて\(x\)座標、\(y\)座標が整数の点を見つけます。
切片からその点まで、右にいくつ動いたか、上下にいくつ動いたかを読み取ります。
読み取りできたら、次の式で傾きを計算できます。
\(\displaystyle \text{傾き} a = \frac{\text{上下の移動量}}{\text{右への移動量}}\)
これで、\(a\)、\(b\)の値がわかるので、\(y=ax+b\)の式に当てはめれば関数の式がわかります。

一次関数のグラフの読み取り方でも一番ネックになるのが、この傾きの使い方です。
ここがわかればグラフを簡単に読み取れるようになります。
別記事でさらに詳しく解説しているので、イメージがしづらければこちらをお読みください。
👉具体例でわかる!グラフ上での傾きの考え方!
例題で一次関数の式の読み取り方を見てみよう
例題1(傾きが整数)
次のグラフの関数の式を求めなさい。
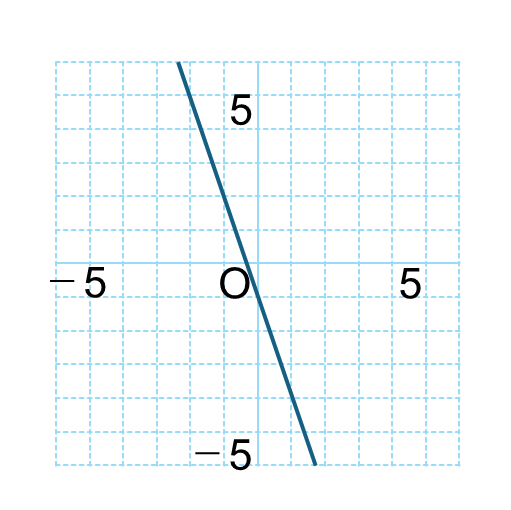
【解説】
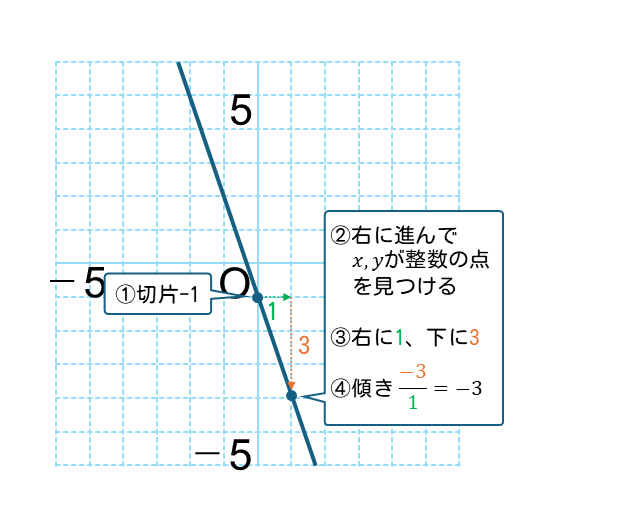
- 切片を読み取る
⇒切片は-1 - 切片から右に移動して、\(x\)座標、\(y\)座標が整数の点を見つける
- 右への移動量、上下の移動量を読み取る
⇒右へ 1、下に 3 - \(\displaystyle \text{傾き}=\frac{\text{上下の移動量}}{\text{右への移動量}}\)
から、傾きを計算する
\(\displaystyle \text{傾き}=\frac{-3}{1}=-3\)
よって関数の式は
\(y=-3x-1\)
例題2(傾きが分数)
次のグラフの関数の式を求めなさい。
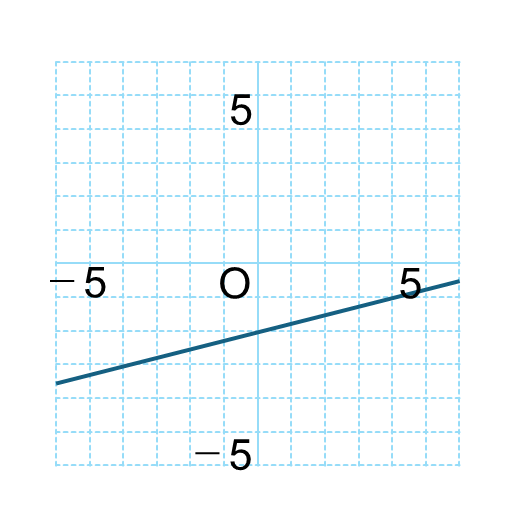
【解説】
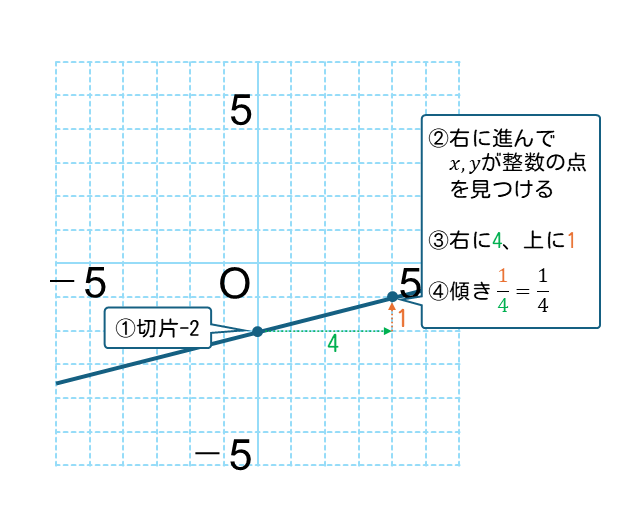
- 切片を読み取る
⇒切片は-2 - 切片から右に移動して、\(x\)座標、\(y\)座標が整数の点を見つける
- 右への移動量、上下の移動量を読み取る
⇒右へ 4、上に 1 - \(\displaystyle \text{傾き}=\frac{\text{上下の移動量}}{\text{右への移動量}}\)
から、傾きを計算する
\(\displaystyle \text{傾き}=\frac{1}{4}\)
よって関数の式は
\(\displaystyle y=\frac{1}{4}x-2\)
【応用】一次関数のグラフから式を考えるときの思考ロジック

ここは、一次関数の学習が一通り済んでから再度読んでいただく方がいいです。
一次関数のグラフから式を考えるときは
- 通る2点がわからないか
- 切片・傾きが読み取れないか
の順で検討する
少し、先の範囲になりますが、通る2点がわかると、関数の式を求めることができます。
そのため、直線のグラフから式を考えるときに、
- 切片・傾きが読み取れないか
- 通る2点がわからないか
のどちらを先に検討するか、自分の中で決めておくとスムーズに問題を解くことができます。
結論を先にお伝えすると、この記事のテーマからは外れますが、「通る2点」から探した方がよいです。
今回取り扱った問題では、グラフの目盛りが読めました。
そのため、「切片⇒傾き」の順で考えることができました。
この範囲は、「グラフ⇒関数の式」とイメージできるようになるためにとても重要です。
しかし、目盛りが読めるタイプの問題は、定期テストでは頻出ですが、実際の入試ではあまり見かけません。
そのため、「通る2点がないか⇒切片・傾きが読み取れないか」の順で検討するようにしておくと、後々の応用が効きやすいのです。
おわりに
この記事では、一次関数のグラフから、関数の式を読み取る方法についての解説しました。
一次関数のグラフを描くときと同じように、グラフの読み取りも「切片⇒傾き」の順で読み取れば大丈夫です。
この基本を押さえておくと、応用問題にもスムーズに取り組むことができます。
グラフの描き方と併せて押さえておくと、さらに理解が深まるので、ぜひセットで学習してみてください。
がんばってください。
【関連記事】
- 切片が分数のグラフの描き方の記事がまだの方はこちら
切片がとれないときは、1点目に適当な整数の点を探して、傾きを使って2点目を探してグラフを描きます。
定期テストでしか出題されませんが、だいたい1題ぐらいは出るので、テスト対策の方はぜひお読みください。
👉【定期テスト向け】切片が分数であるグラフの描き方 - 切片分数のグラフの描き方を読んだ方または不要な方の、次の記事はこちら
直線の式のほとんどは一次関数ですが、例外が2つあります。
それが\(「x=a」,「y=b」\)のグラフです。
このグラフの意味や、グラフの描き方、直線のグラフの考え方などについて解説します。
👉一次関数ではない直線「x=a」「y=b」をていねいに解説 - 一次関数のまとめに戻る方はこちら
関数は、抽象的で取り組みづらい反面、同じ操作が繰り返し出てくるので、コツが掴めると得意にしやすい分野でもあります。
考え方からていねいに解説しているので、ぜひ先々まで活用できるかたちで知識を身に付けてください。
👉【完全攻略】一次関数の解き方・考え方を基礎からじっくり


コメント