【定期テスト対策・中2数学】一次関数のグラフ上の点の求め方をやさしく解説

「グラフ上の点の求め方がわからない」
そんな経験ないですか？

求め方はシンプルなのに、意外と求め方を忘れてしまうのが、グラフ上の点の求め方。
一次関数のグラフ上の点は「式に代入するだけ」で必ず求められます。
定期テスト、入試、ともにほぼ間違いなく出る問題なので、できるようにすれば得点アップ間違いなしです。

今回の記事では、グラフ上の点の求め方や、その考え方について解説します。

グラフ上の点はどうやって求めたらいい？

グラフ上の点は関数の式に代入して求める

一次関数の点の求め方を具体例で確認しよう

次の図の点Pを求めてみます。

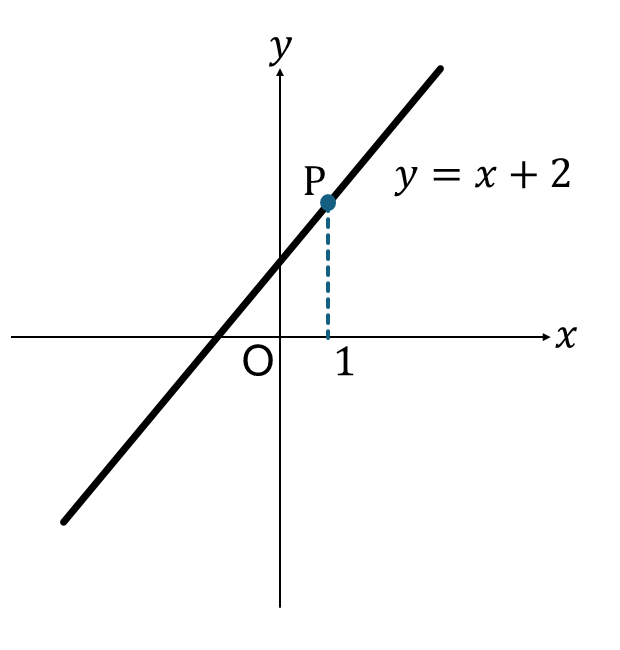
点Pは、\(y=x+2\)上の点で、\(x\)座標は1です。
そのため、\(y\)座標は、\(y=x+2\)に\(x=1\)を代入すれば求めることができます。

\(y=1+2 \\ y =3\)

よって、点Pは、P(1, 3)となります。

また、次の図の点Pを求めてみます。

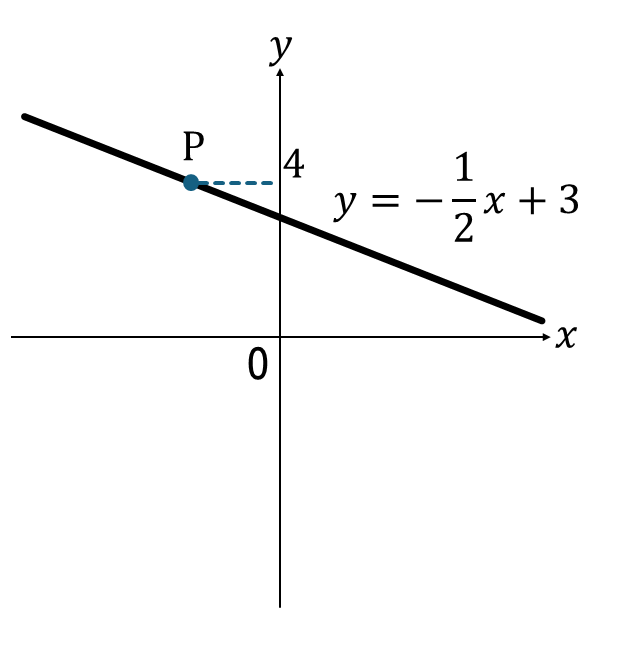
点Pは、\(\displaystyle y=-\frac{1}{2}x+3\)上の点で、\(y\)座標は4です。
そのため、\(y\)座標は、\(\displaystyle y=-\frac{1}{2}x+3\)に\(y=4\)を代入すれば求めることができます。

\(\displaystyle 4=-\frac{1}{2}x+3 \\ \displaystyle \frac{1}{2}x = 3-4 \\ \displaystyle \frac{1}{2}x = -1 \\ x = -2\)

よって点Pは、P(－2,4)となります。

例題で考えてみよう！

例題1（\(y\)座標を求める問題）

次の図の点Pを求めなさい。

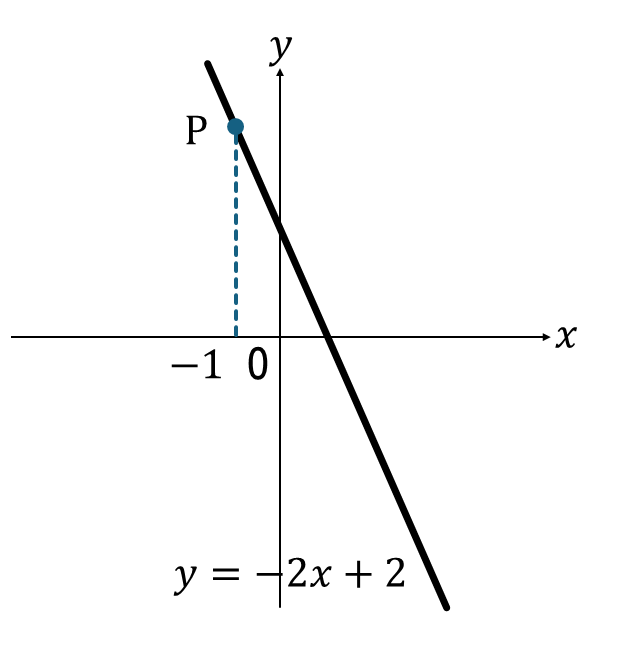
【解説】

グラフの式\(y=2x+2\)に\(x=-1\)\を代入して

\(y=-2 \times (-1)+2 \\ y =2+2 \\ y=4 \)

よって、点P(－1, 4)

例題2（\(x\)座標を求める問題）

次の図の点Pを求めなさい。

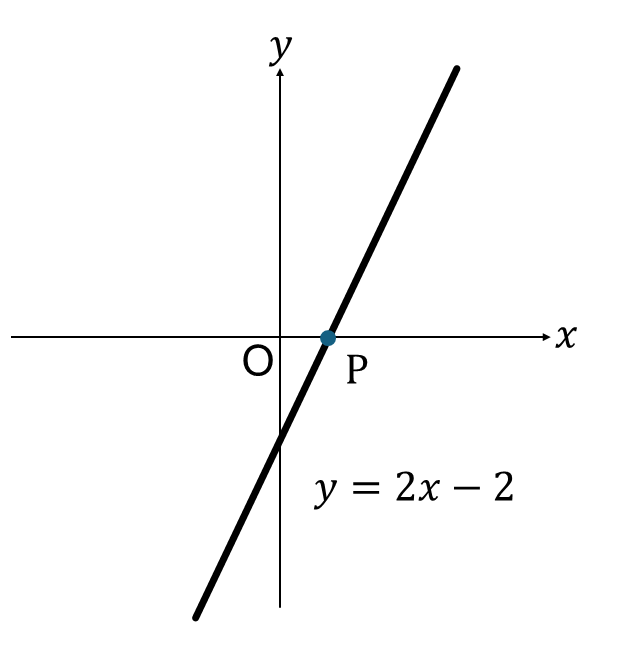
【解説】

\(x\)軸上の点の\(y\)座標は0です。

グラフの式\(y=2x-2\)に\(y=0\)\を代入して

\(0=2x-2 \\ 2x =2 \\ x=1 \)

よって、点P(1, 0)

\(x\)軸上の点の\(y\)座標が0は、慣れていないと忘れがちです。
もう一度、「\(y\)座標は \(x\)軸からどれだけ離れているかを表している」という基本を振り返ってみてください。

関数の式から座標を求めるときの思考メソッド

グラフ上の点を求める
⇒グラフの式に代入
⇒グラフの式と\(x\)または\(y\)を探す

グラフから、点の座標を求める方法のほとんどはグラフの式に代入して求めます。

そのため、「グラフ上の点を求める⇒グラフの式に代入」という考えの型がすぐに出てくることが大切です。

また、グラフの式に代入するためには、グラフの式と、\(x\)または\(y\)の値が必要です。
だから、問題からグラフ式と、\(x\)または\(y\)の値を探さなければいけません。

何が必要かわかったうえで探すと、いまいち必要性がわからず条件を整理していくのに比べて、効率もテスト当日の余裕も違います。

だから、「グラフの点を求めさい」という問題が出たら、「グラフの式に代入⇒グラフの式と\(x\)または\(y\)を探す」という流れがセットで出てくるようにしておくとよいです。

関数の式から\(x,y\)を計算する方法との関係

グラフ上の点を求める方法と、関数の式から\(x,y\)を計算する方法は、全く同じです。
それは、グラフは「関数の式を満たす点の集まり」だからです。
グラフ上の点を求めることと、関数の式を満たす\(x,y\)を求めることは、関数の見方が違うだけで、まったく同じ操作なのです。

こちらの記事で、「グラフが式を満たす点のあつまり」の意味について解説しています。
根拠がわかれば、計算方法も忘れにくくなるので、ぜひ読んでみてください。
👉「グラフは式を満たす点のあつまり」の意味を比例のグラフでやさしく解説

おわりに

今回の記事では、グラフ上の点を計算する方法について解説しました。

基本問題で出ることもありますし、応用問題の途中として出ることもある、とても大事な範囲です。
「座標の求める」⇒関数の式に代入⇒関数の式、\(x\)座標または\(y\)座標を探す」という考え方が定着できるように、しっかり練習してみてください。

また、グラフの意味について学習を深めると、関数の式から\(x\)、\(y\)を計算するときと方法が同じである理由など、学びが深まります。
併せて学習してみてください。