「解説を見れば『ああ、なるほど』と思う。でも、白紙の答案を前にすると、ペンが止まってしまう……」
そんな経験、ありませんか?
実は、数学が得意な人と苦手な人の違いは、計算力ではありません。
「考え始める順番」が違うだけなのです。
数学には、答えを出すための「思考のルート」があります。
この記事では、応用問題を解くために必須となる「逆算の考え方」について紹介します。
逆算の考え方ってどうやったらいいの?
数学の問題を考えるときは、「求めたいもの」から逆算して考えていくのが基本です。
具体的には、次の順に思考、情報を整理します。
なぜ「求めたいもの」⇒「条件」の順に考えるのか?
数学の問題では、問題文に条件が書いてあるので、「どの条件を使うか」とい発想をする人が多いと思います。
しかし、条件はたくさんあることが普通で、使う順序も違います。
だから、公式を一度使うだけの簡単な問題なら条件から考えてもいいのですが、難易度が上がると何をどこから使えばいいのか混乱してしまうのです。
一方、求めたいものは1つしかありません。
(複数の答えを求める問題でも、1つずつに分けて考えればいいだけなので)
また、求めるための方法も決まっています。
そのため、求めたいものをスタートにして考えると、何をどの順序で考えればいいのかが整理しやすくなるのです。
例題で逆算の考え方を確認しよう
例題1(逆算の必要がない問題)
底辺2、高さ4の三角形の面積を求めなさい。
【解説】
三角形の面積の公式に当てはめて
2 × 4 ÷ 2 = 4

解説の必要もないような例題ですね。
このような公式を一度使うだけの問題では、逆算する必要はありません。
例題2(逆算した方がわかりやすい問題)
下図の△OAPの面積を求めなさい。
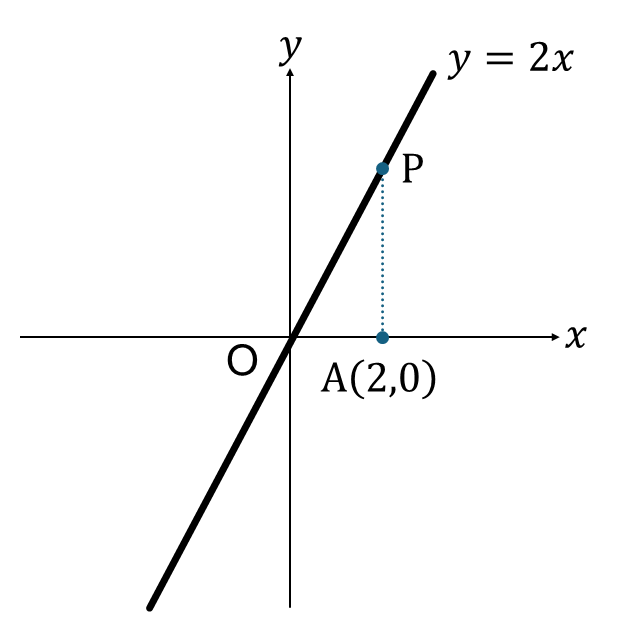
【解説】
このような問題になると、「どうやって考えたらいいの?」と思う人が増えると思います。
ここでこそ、逆算の考え方が役立ちます。
求めたいものから、何が必要かを考えていきます。
- 求めたいものが何かを考える
今回、求めたいものは「三角形の面積」 - 求めたいものを計算するための公式、必要な情報を考える
面積の公式は(底辺)×(高さ)÷ 2
なので、底辺、高さが必要
⇒底辺をOA、高さをAPとみる - 条件から必要な情報を読み取る
- 底辺OAは\(x\)座標から2とわかる
- 高さAPは点Pの\(y\)座標
⇒\(y=2x\)に\(x\)=2を代入して\(y\)座標を求める
これをもとに解答をつくると、次のようになります。
点Aの座標が(2, 0)なので
OA = 2
点Pの座標は、\(y=2x\)に\(x=2\)を代入して
点P(2, 4)
よって、AP = 4
求める面積は
(底辺)×(高さ)÷ 2
= 2 × 4 ÷ 2
= 4
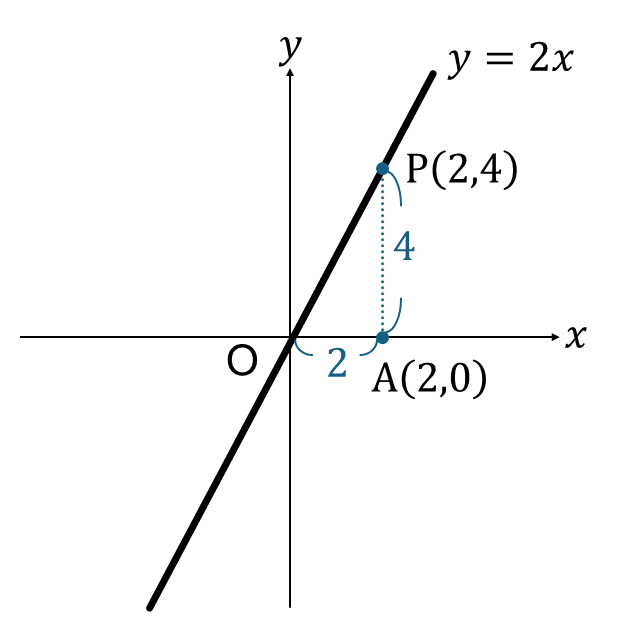
「思考の順序」と「解答の順序」は別物
例題2の「思考の順序」と「解答の順序」を比べてみてください。
2つの順序が一致していないことがわかると思います。
実は、「思考の順序」と「解答の順序」は一致しないことが多いです。
- 考えるとき
⇒「求めたいもの」から逆にたどる - 書く(説明する)とき
⇒「与えられた条件」から順に進める
という違いがあるからです。
この違いがあるので、「解説は理解できるけど、問題が解けない」ということが起こってくるのです。
さきほどの例題2であれば、逆算する人と、しない人で解説の読み方は次のように違います。

まず、OAを求めて、次にAPを求めて、公式を使うのか!

面積を求めるためには、底辺と高さが必要…
だから、OAとAPを求めているんだ!
逆算することのもう1つの利点
逆算の考え方をすることには、思考を整理しやすくする以外にもう1つ利点があります。
それは、他の問題への応用が利きやすいということです。
もう1度、先ほどの例題2を思い出してください。
逆算して考える人だと、「面積を求める」という目的が同じであれば、条件が違う他の問題にも考え方を応用していくことができます。
しかし、逆算しない人のように「条件」から考え始めていると、条件が変わってしまえば途端に応用しにくい知識に変わってしまいます。
そうすると、「問題の数だけ解き方を覚える」ということになってしまいます。
高校受験ぐらいのレベルであれば、記憶力次第でそれでも何とか通用します。
しかし、大学受験のレベルになると、それで問題を解決できる人はほとんどいないと思います。

「中学校まではできたけど、高校になると授業についていけなくなる」というのは本当によくあります。
ぼくの知っている範囲では、高校受験をパターン暗記に頼り切りって、そこで止まってしまった人が多いです。
パターン暗記は、「合格」という目標に対してはわりと最短ルートなんですが、その先の応用まで見据えると、かなりの遠回りになってしまいます。
逆算の考え方を身につけるための習慣
いきなり、逆算の考え方を身に付けるのは難しいと思いますが、すぐにできる習慣が1つあります。
それは、わからない問題があったときに、「どうやって考えればいいのか?」ではなく、「どこから考え始めればいいのか?」という視点で解説を見るようにすることです。
考え始めが正しければ、後は順に論理を展開していけば、方針が何となく見えてきます。
一番大切なのが、最初の考え始めの部分なのです。
それを繰り返していけば、少しずつ“逆算思考”の感覚が身についていきます。
おわりに
数学の勉強は、ついつい「答えを出すこと」ばかりに目が向きがちです。
しかし、本当に大切なのは、答えに至るまでの「道筋をどうやって見つけたか」という部分にあります。
もし、テストや自習で解けない問題に出会ったら、ガッカリする必要はありません。
それは新しい「考え始めのポイント」を学ぶチャンスです。
今回紹介した「逆算思考」を意識して、解説を「答え合わせ」ではなく「思考の答え合わせ」として使ってみてください。
そうすれば、条件から正答までの道筋が、あなたの頭の中に描けるようになっていきますよ。


コメント