一次関数の式を求める問題は、定期テスト・入試の頻出テーマです。
与えられる条件に戸惑うかもしれませんが、実は解法は「たった3つのパターン」に集約されます。
この記事では、その3パターンと解法の基本を解説し、
厳選された演習問題を通じて、どんな出題条件でも正確に式を求められる実戦力を養います。
今日で一次関数の式を完全にマスターしましょう!
【関連記事】
- 一次関数の式の求め方について詳しく知りたい方はこちら
一次関数の式の求め方は、パターンが限られています。
しっかりパターンを押さえれば、必ずできるようになるので、
まだの方はぜひお読みください。
👉【3パターン】一次関数の式の求め方を例題付きでていねいに解説
一次関数(直線)の式の求め方|前提知識
一次関数の式を求める問題の出題パターンと解き方は、大きく次の3つに分けられます。

ここからは、この知識を使って問題を解いていきます。
一次関数の式の求め方を例題で確認
例題
それぞれ、次の式を求めなさい。
1)2点(-1, 4) , (1, 2) を通る直線の式
2)傾きが2で、点(2, 3)を通る直線の式
3)切片が1で、点(4, 2)を通る直線の式
【解説】
1)
求める直線の式を\(y=ax+b\)とおくと
\(x=1,y=2\)を代入すると
\(2=a+b\)…①
\(x=2,y=4\)を代入すると
\(4=-a+b\)…②
\(\begin{array}{l} a+b=2 …① \\ -a+b=4 …② \end{array}\)
①-②を計算すると
\(2a=-2 \\ a=-1\)
①に代入して
\(2=-1+b \\ b=3\)
よって求める直線の式は、
元の式に\(a,b\)の値を代入して
\(y=-x+3\)

式を求めるときは、定数項が必ず\(b\)なので、加減法で求めるのがはやいし、正確です。
2)
傾きが2なので、直線の式は
\(y=2x+b\)とおける
\(x=2,y=3\)を代入して
\(3=2 \times 2 +b \\ b= -1\)
よって求める直線の式は
元の式に\(b\)の値を代入して
\(y=2x-1\)
3)
切片が1なので、直線の式は
\(y=ax+1\)とおける
\(x=4,y=2\)を代入して
\(2=4a+1 \\ 4a=1\\ \displaystyle a = \frac{1}{4}\)
よって求める直線の式は
元の式に\(a\)の値を代入して
\( \displaystyle y = \frac{1}{4}x + 1\)
演習問題で一次関数の式の求め方を網羅

どのパターンで出ても落ち着いて解けるように、
あえてパターンはばらばらにしています。
演習1
\(x=-2\)のとき\(y=1\)、
\(x=1\)のとき\(y=-5\)である一次関数の式を求めなさい。
解説
求める直線の式を\(y=ax+b\)とおくと
\(1=-2a+b\)…①(\(x=-2,y=1\)を代入)
\(-5=a+b\)…②(\(x=1,y=-5\)を代入)
①-②を計算すると
\(6 = -3a \\ a= -2\)
①に\(a\)の値を代入すると
\(1=-2 \times (-2) +b \\ 1=4+b \\ b=-3 \)
よって求める直線の方程式は
\(y=-2x-3\)
演習2
切片が3で、点(-1,-2)を通る直線の式を求めなさい。
解説
切片3
⇒\(y=ax+3\)とおくと
\(-2=-a+3\)(\(x=-1,y=-2\)を代入)
\(a=3+2 \\ a=5\)
よって求める直線の方程式は
\(y=5x+3\)
演習3
傾きが4で、点(2, 6)を通る直線の式を求めなさい。
解説
傾き4
⇒\(y=4x+b\)とおくと
\(6=4 \times 2+b\)(\(x=2,y=6\)を代入)
\(6=8+b \\ b=-2\)
よって求める直線の方程式は
\(y=4x-2\)
演習4
変化の割合が3で、\(x=3\)のとき\(y=4\)である一次関数の式を求めなさい。
解説
変化の割合と傾きは同じ値
変化の割合が3
⇒\(y=3x+b\)とおくと
\(4=3 \times 3+b\)(\(x=3,y=4\)を代入)
\(4=9+b \\ b=-5\)
よって求める直線の方程式は
\(y=3x-5\)
演習5
2点(0, 2) , (1, 3)を通る直線の式を求めなさい。
解説
求める直線の式を\(y=ax+b\)とおくと
\(2=b\)…①(\(x=0,y=2\)を代入)
\(3=a+b\)…②(\(x=1,y=3\)を代入)
②に\(b=2\)を代入すると
\(3 =a+2 \\ a= 1\)
よって求める直線の方程式は
\(y=x+1\)

点(0, 2)は\(x\)座標が0なので、\(y\)軸上の点、つまり切片です。
ただ、この問題のように2点の形で条件が与えられたときは、2点が与えられたときの処理で対処した方がいいです。
理由は次の問題で説明します。
演習6
2点(-1, 6) , (2, 0)を通る直線の式を求めなさい。
解説
求める直線の式を\(y=ax+b\)とおくと
\(6=-a+b\)…①(\(x=-1,y=6\)を代入)
\(0=2a+b\)…②(\(x=2,y=0\)を代入)
①-②を計算すると
\(6=-3a \\ a=-2\)
①に\(a\)の値を代入すると
\(6=-(-2)+b \\6 = 2+b \\ b=4\)
よって求める直線の方程式は
\(y=-2x+4\)

点(2, 0)は\(y\)座標が0なので、\(x\)軸との交点です。
テスト中であわてていたりすると、切片と読み間違えることがあります。
一般形でおいて、\(x,y\)を間違えずに代入するように習慣づけると、あわててミスすることが減ります。
演習7
点(2,3)を通り、直線\(\displaystyle y = \frac{1}{2}x+1\)と平行な直線を求めなさい。
解説
平行な2直線の傾きは同じ
直線\(\displaystyle y = \frac{1}{2}x+1\)と平行
⇒傾きが\(\displaystyle \frac{1}{2}\)
\(\displaystyle y=\frac{1}{2}x+b\)とおくと
\(\displaystyle 3=\frac{1}{2} \times 2 +b\)(\(x=2,y=3\)を代入)
\(3=1+b \\ b=2\)
よって求める直線の方程式は
\(\displaystyle y=\frac{1}{2}x+2\)
演習8
下図の直線の式を求めなさい。
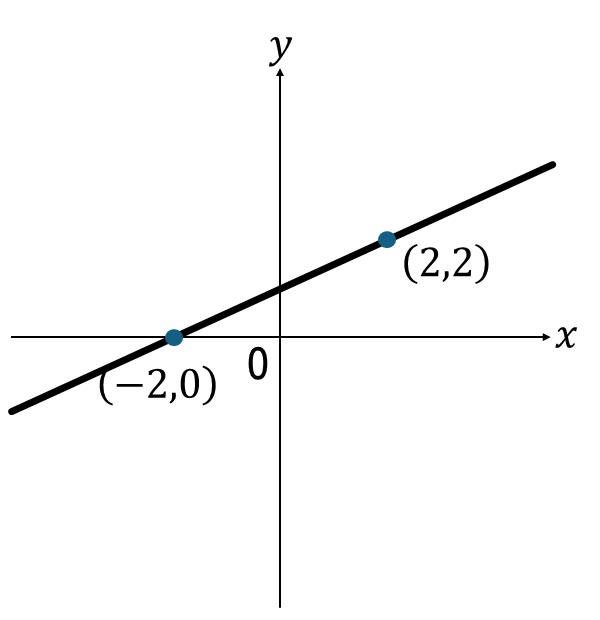
解説
求める直線の式を\(y=ax+b\)とおくと
\(2=2a+b\)…①(\(x=2,y=2\)を代入)
\(0=-2a+b\)…②(\(x=-2,y=0\)を代入)
①-②を計算すると
\(2=4a \\ \displaystyle a=\frac{1}{2}\)
①に\(a\)の値を代入すると
\(2=1+b \\ b=1\)
よって求める直線の方程式は
\( \displaystyle y=\frac{1}{2}x+1\)
【別解】
左の点から右の点まで
\(x\)座標が4増加
\(y\)座標が2増加
よって傾きは
\(\displaystyle \text{傾き}=\frac{\text{yの増加量}}{\text{xの増加量}}=\frac{2}{4}=\frac{1}{2}\)
求める式を
\(\displaystyle y= \frac{1}{2}x+b\)
とおくと
\(\displaystyle 2= 1+b \\ b = 1\)
よって求める直線の方程式は
\( \displaystyle y=\frac{1}{2}x+1\)

図があるから特別この解法ができるというわけでもありません。
演習1、5みたいな問題でも、当然同じ解法で解くことができますが、グラフがないとイメージが追い付かないと思うので、あえて載せていません。
(どっちの解法も意味的には同じ)
こちらの記事で、2つの解法がどういう関係にあるのか、メリット・デメリットを比較しているので興味があったら読んでみてください。
👉一次関数2点から式を求める2つの解法を徹底比較!【中2数学】
演習9
下図の直線の式を求めなさい。
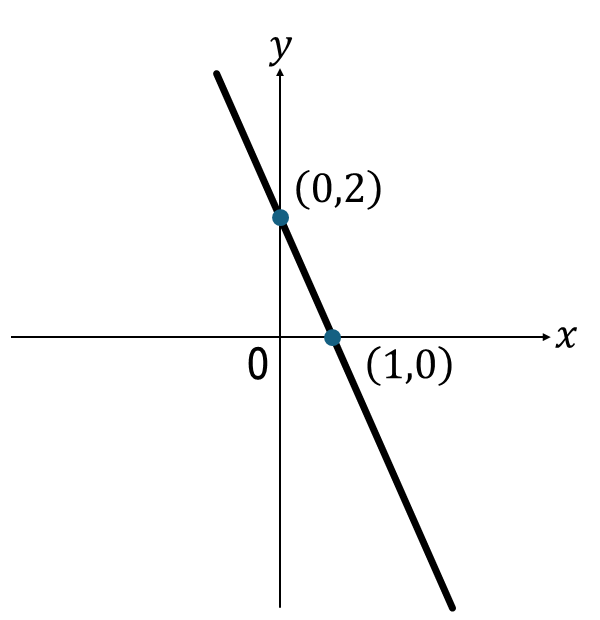
解説
求める直線の式を\(y=ax+b\)とおくと
\(2=b\)…①(\(x=0,y=2\)を代入)
\(0=a+b\)…②(\(x=1,y=0\)を代入)
①より
\(b=2\)
②に代入して
\(0=a+2 \\ a = -2\)
よって求める直線の方程式は
\( y=-2x+2\)
【別解】
左の点から右の点まで
\(x\)座標が1増加
\(y\)座標が-2増加
よって傾きは
\(\displaystyle \text{傾き}=\frac{\text{yの増加量}}{\text{xの増加量}}=\frac{-2}{1}=-2\)
また、図より切片が2
よって求める直線の方程式は
\( \displaystyle y=-2x+2\)
おわりに
お疲れ様でした!
この記事では、一次関数の式の求め方の3つの基本パターンから、
傾きと変化の割合、平行な直線の関係、さらにはグラフからの読み取りまで、
幅広く演習を行いました。
一次関数は、\(y=ax+b\)という基本形に立ち返り、与えられた条件を使って傾き\(a\)と切片 \(b\)を求めることがすべてです。
もし、解き方を忘れてしまっても、
連立方程式で解くか、切片や傾きを先に代入して解くかの2つのアプローチを思い出せば、
必ず答えにたどり着けます。
解き方をしっかり定着させ、テスト本番で得点源にできるよう、繰り返し練習してください!
【関連記事】
- 一次関数の式の求め方について詳しく知りたい方はこちら
一次関数の式の求め方は、パターンが限られています。
しっかりパターンを押さえれば、必ずできるようになるので、
まだの方はぜひお読みください。
👉【3パターン】一次関数の式の求め方を例題付きでていねいに解説 - 2点が与えられたパターンの問題の解法について詳しく知りたい方はこちら
この記事で解説した、2点を与えられたパータンの問題の、「\(y=ax+b\とおく」解法と、「変化の割合を使う」解法の比較記事です。
2つが同じものであるという根拠、メリット、デメリットや、どう使い分けるべきかについて解説しています。
一次関数への理解を深めたい方は、ぜひ読んでみてください。
👉一次関数2点から式を求める2つの解法を徹底比較!【中2数学】 - 傾きにとグラフ上の点の動き方の関係がイメージしづらい方はこちら
一次関数のグラフ上の点は、傾きの分母の数だけ右に、傾きの分子の数だけ上下に動きます。
ここがわかると、傾きの数字から、グラフがどういう形状になっているかイメージしやすくなります。
こちらの記事で具体例付きで解説しているので、ぜひ読んでみてください。
👉傾きによるグラフの動き方についての補足記事 - 連立方程式の加減法を復習したい方はこちら
今回の記事で使った、連立方程式の加減法について解説しています。
解き方や、間違えやすいポイントに加え、なぜひっ算で求めることができるのかについて、くわしく説明しているので、ぜひ一度読んでみてください。
👉連立方程式の意味と解法!加減法と代入法をマスターしよう


コメント