【基礎・中2数学】一次関数と連立方程式の関係、交点の求め方をわかりやすく解説

一次関数と連立方程式、一見するとまったく別の単元に見えます。
でも、実は深くつながっています。

二元一次方程式を変形すれば一次関数の形になります。
そして、連立方程式の解はグラフの交点になっています。

この記事では、

• 二元一次方程式と一次関数の関係
• 2つの一次関数のグラフの交点の求め方

を、例と図を使ってわかりやすく解説します。
関数と方程式のつながりを、いっしょに整理していきましょう。

二元一次方程式と一次関数ってどういう関係？

二元一次方程式と一次関数は同じもの

なぜ二元一次方程式と一次関数は同じと言える？

二元一次方程式って何？

「元」、「次」の意味はそれぞれ次の通りです。

• 元
  方程式に含まれる文字の種類のこと。
• 次
  方程式中の文字の最高の次数のこと。

つまり、二元一次方程式とは
「文字の種類が2種類、文字の最高次数が1次の方程式」
のことを言います。

たとえば、次のような式が挙げられます。

\(x-2y=2\)

「連立方程式で出てきた方程式」と思うとイメージしやすいと思います。

\(y\)について解くとどうなる？

この式を\(y\)について解くと

\(x-2y=2 \\ -2y=-x+2\\ \displaystyle y=\frac{1}{2}x-1\)

これで一次関数の式と同じ形になりました。

二元一次方程式と一次関数の式は表し方が違うだけ

変形すると同じ形にできるのだから、結局、「二元一次方程式」と「一次関数の式」は同じものだったということです。

「\(y=○\)」の形は、グラフを描いて視覚的に捉えやすいです。
だから、「グラフを使いたいときに変形する」と思っておくとよいです。

グラフの交点ってどうやって求めたらいい？

グラフの交点の座標は、グラフの式の連立方程式の解

交点の求め方はすごく大事なポイントです。
必ずできるようにしておきましょう。

交点の求め方を具体例で見てみよう

たとえば、次の①、②の交点を求めてみます。

\(y=2x-1\)…①
\(y=x+2\)…②

①を②に代入すると

\(2x-1=x+2 \\ x=3\)

①に\(x=3\)を代入して

\(y=2 \timex 3 -1 \\ y = 5\)

よって交点は\((3,5)\)と求めることができます。

交点を求める計算のコツ

関数の式は必ず「\(y=○\)」の形で表されているので、代入法を使ったほうが速く計算できて、ミスも少ないです。

代入法と大げさに言いましたが、式の右辺同士をイコールでつないでいるだけです。

連立方程式を習う順番が「加減法⇒代入法」の順番が一般的なので、代入法と聞くと食わず嫌いをする人をときどき見かけますが、ここは絶対代入法がよいです。

なぜ連立方程式の解がグラフの交点になるの？

グラフは「式を満たす点のあつまり」です。
だから、グラフの交点の座標は、「2つのグラフの式を同時に満たす\(x,y\)」になっています。

一方、連立方程式の解も「2つの式を同時に満たす\(x,y\)」です。

結局、グラフの交点も連立方程式も「2つの式を同時に満たす\(x,y\)」のことを指しています。
つまり同じものであるということです。

なぜ連立方程式の解がグラフの交点になるのか、具体例付きで解説した記事です。
もう少し詳しく知りたい方はこちらの記事をお読みください。
👉連立で交点がわかる理由！交点と連立方程式の意味からわかりやすく解説

グラフの交点を考えるときの思考ロジック

「グラフの交点⇒関数の式を連立⇒関数の式を探す」という考え方の型を持っておいてください。

グラフの交点は、連立させる以外に求め方はありません。
だから、必ず関数の式が必要になります。

難しい問題になると、関数の式が決まっておらず、式を自分で求める必要があるときがあります。
しかし、「交点⇒連立⇒関数の式が必要」と考えられれば、迷わず関数の式を求めにいくことができます。

グラフから読み取って連立方程式の解を求める方法

グラフの交点を読めば連立方程式の解がわかる

目盛り付きの用紙を使う場合、次の手順で連立方程式の解を求めることができます。

連立方程式のグラフを用いた解き方を具体例で見てみよう

\(2x-y=-1\)…①
\(x+y=-5\)…②

という2つ二元一次方程式の連立方程式を考えます。
それぞれ、\(y\)について解くと、次のように変形できます。

\(y=2x+1\)…①’
\(y=-x-5\)…②’

これをグラフ用紙に描いて、目盛りを読むと
交点は\(-2,-3\)と読み取ることができます。
（下図参照）

だから、元の連立方程式の解は
\(x=-2,y=-3\)
と求められます。

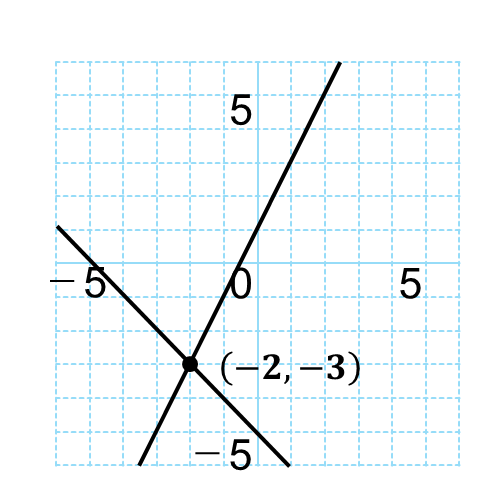
おわりに

今回の記事では、一次関数と連立方程式についてみていきました。

「二元一次方程式」と「一次関数の式」は同じもので、「連立方程式の解」と「グラフの交点」は同じものでした。

特に、「交点を求めるときは連立させる」は、一次関数に限った話ではありません。
中3の二次関数や、高校で習う関数でも、すべての交点は連立させて求めます。

この先の勉強の基礎になる部分なので、しっかりマスターしてください。
がんばってください。

← 一つ前のページに戻る