【関数の基礎】連立で交点がわかる理由！交点と連立方程式の意味からわかりやすく解説

グラフの交点を求めるときは、グラフを連立させます。
この「交点⇒連立」の考え方は、関数の種類に関わらず常に同じです。

何となく、「交点の求め方は連立」とだけ覚えて終わってしまう人も多いところですが、
根拠から理解できると、関数への理解がぐっと深まります。

この記事では、なぜグラフの式を連立させると交点を求められるのかの根拠について、
交点の意味、連立方程式の意味から具体例を用いて解説していきます。

なぜ交点は式を連立させると求められるの？

交点の座標と連立方程式の解は同じ意味だから

交点、連立方程式の意味から「交点⇒連立」の根拠を考える

グラフと交点の意味

グラフは、関数の式を満たす点の集まりです。
だから、グラフ上の点の座標は、必ずそのグラフの式を満たします。

また、交点は2つのグラフ上で重なっている点のことです。
だから交点はの座標は、それぞれの関数の式を満たします。

たとえば、次の2式の交点を考えます。

\(y=2x+1\)…①
\(y=-x-5\)…②

このグラフの交点は\((-2,-3)\)ですが、
それぞれの式に\(x=-2,y=-3\)を代入すると

①の式は
\(y=2x+1 \\ -3 = 2 \times (-2) + 1 \\ -3 = -3\)
②の式は
\(y=-x-5 \\ -3 = -(-2)-3 \\ -3 = -3\)

となり、交点の座標どちらの式も満たしていることがわかります。

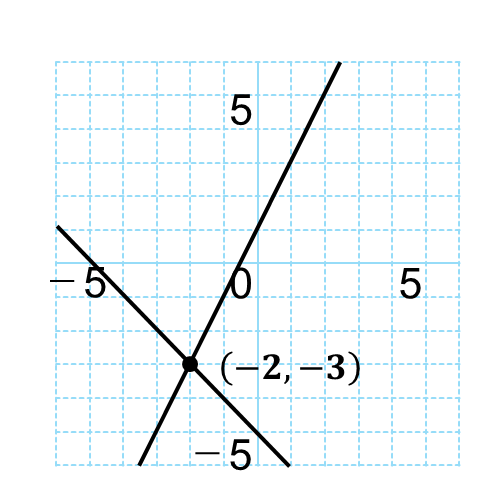
連立方程式の意味

解き方が複雑なので意味を忘れがちかもしれませんが、
連立方程式は、そもそも「2式を同時に満たす\(x,y\)を求めるための解き方」です。

加減法、代入法のどちらも、
「\(x,y\)はどちらの式でも共通の値である」
という前提で成り立っています。

たとえば、次のような連立方程式では、

\(2x+3y=1\)…①
\(x+3y=-2\)…②

①－②を計算して

\(x=3\)

のように計算をすると思います。
この計算では、\(x,y\)の項について

\(2x-x=x\)
\(3y-3y=0\)

と計算していますが、もし\(x,y\)が①、②の式でそれぞれ違う値であれば、
このような計算が成り立たなくなるのです。

代入方も同じで、次のような方程式で

\(y=2x-1\)…①
\(3x+2y=1\)…②

①を②に代入して

\(3x+2(2x-1)=1\)

と計算しますが、この計算も①と②の\(y\)が違う値であれば成り立ちません。

だから交点は連立方程式で求められる

ここまでで見た通り、連立方程式の解は2式を同時に満たす\(x,y\)になっているのです。

まとめると、交点の座標、連立方程式の解の意味は次のようになり、
同じものであるということがわかります。

• 交点の座標：2式を同時に満たす\(x,y\)
• 連立方程式の解：2式を同時に満たす\(x,y\)

だから、交点を求めたいときは、連立させてその解を求めるのです。

一次関数以外への適用：「交点⇒連立」はすべての関数に通じる

先ほどの説明は、すべて一次関数を例にしましたが、
交点の座標の意味、連立方程式の意味は、一次関数以外の関数であっても変わりません。

また、中学校2年生の段階では、二元一次方程式の連立方程式しか扱っていませんが、
学習が進むと、どんな方程式でも連立させて解く機会があります。

つまり、一次関数以外の関数でも、交点を求めたいときは連立させて解けばよいということになります。

たとえば、中学校3年生では

\(y=x^2\)…①
\(y=x+2\)…②

の交点を求める機会がありますが、これも連立させて解きます。

①を②に代入して

\(x^2=x+2 \\ x^2-x-2=0\)

ここから二次方程式として解いて、交点を求めます。
（二次方程式の解き方も中学校3年生で習います）

根拠からしっかりわかって「交点⇒連立」と押さえておくと、すべての関数に役立つ知識にするこおとができるのです。

おわりに

この記事では、交点を求めるときに式を連立させる根拠について解説しました。

• グラフは式を満たす点のあつまりである
• 交点が2式を同時に満たす点である
• 連立方程式が2式に共通する\(x,y\)を求める計算方法である

という、3つの基本をしっかり押さえると、その根拠が見えてきます。

根拠からしっかり押さえると、他の関数にも応用することができます。
どんな関数を学習していても、交点を求める機会は必ずあります。

ここがわかると、関数の理解がぐっと進むので、しっかりがんばってください。

← 一つ前のページに戻る