「点A、どうやって求めたらいいの?」
こんな経験ないでしょうか?
高校受験の大問では、ほとんどと言っていいほど出題される関数の問題。
その途中で、必ずグラフ上の点を求める小問が出ます。
しかし、塾講師のころ、計算の手順が整理できていなくて、すっと解き方が出てこず、手が止まってしまう生徒もときどき見かけました。
この記事では、グラフ上の点の求め方について、くわしく解説していきます。
グラフ上の点の求め方の基本
グラフ上で、計算で求めることのできる点は、
- グラフ上の点で\(x\)座標または\(y\)座標がわかっている点
- グラフの交点
のどちらかです。
まず、「グラフ上の点で\(x\)座標または\(y\)座標がわかっている点」について見ていきましょう。

グラフは、「関数の式を満たす\(x\)、\(y\)の集まりである」ということを押さえておくと、説明もすっと入りやすいと思います。
関数の式を使って点を求める方法(xやyがわかっているとき)
グラフは、関数の式を満たす点の集まりです。
だから、
- 関数の式に\(x\)座標を代入
⇒その点の\(y\)座標が計算で求まる - 関数の式に\(y\)座標を代入
⇒その点の\(x\)座標が計算で求まる
ということが言えます。
(次の図を参照)
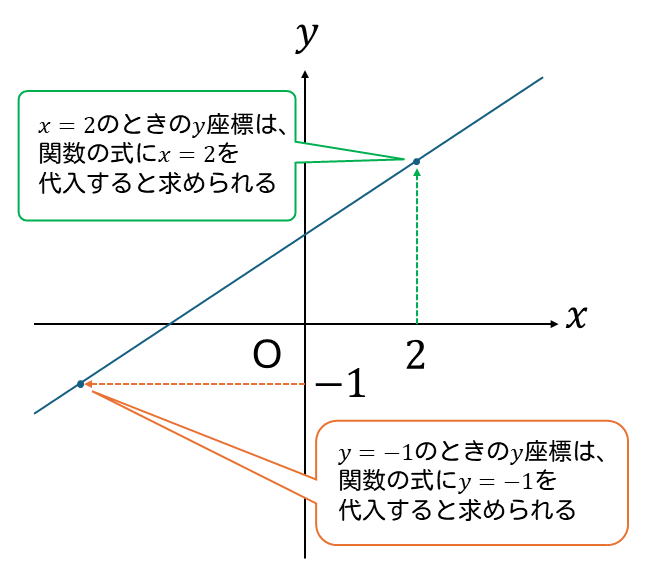
一次関数のx軸上の点
気をつけたいのが、直線の\(x\)軸上の点です。
\(x\)軸は\(y=0\)と表されるため、一次関数の式に\(y=0\)を代入して計算すると求めることができます。
(次の図を参照)
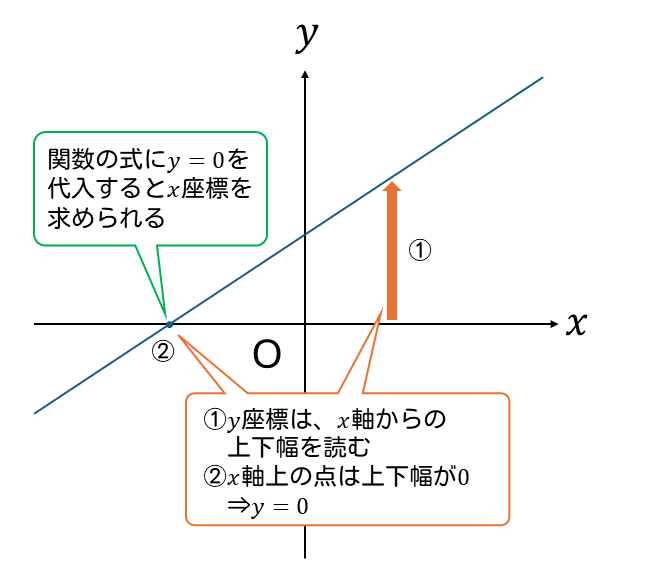

ときどき\(x=0\)とする人がいるので注意してください。
交点の求め方
2つのグラフの交点を求めるときは、グラフの式を連立させてください。
グラフの交点は、2つのグラフが重なる点です。
言い換えると、2つの式を同時に満たす点のことです。
つまり、その交点の座標 \((x,y)\)は、どちらの式に代入しても同じ値になる組み合わせになります。
だから、交点は「2つの式を連立して解く」ことで求められるんです。
これには、関数の式の種類は関係なく、反比例、一次関数、二次関数、どんな関数であっても、連立させれば交点は求まります。

関数の式は「y=〇」の形になっているので、代入法で解くといいですよ。
例題で確認しよう
例題1(一次関数のグラフの点)
次の図の、\(a\)を求めなさい。
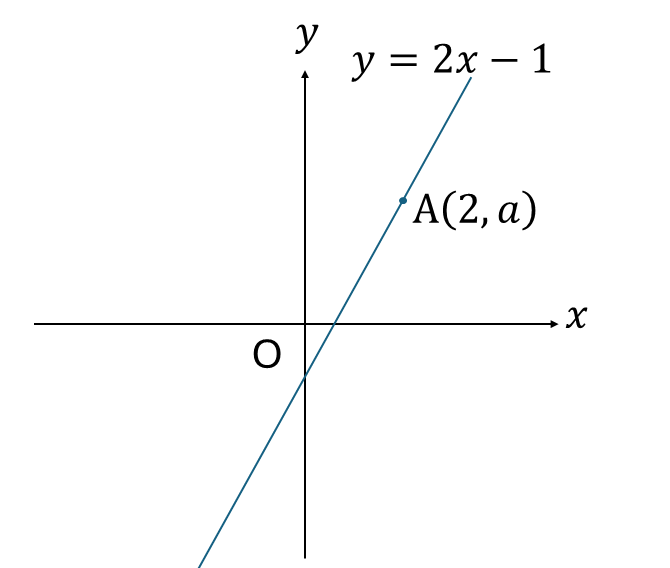
解説
点Aは、\(y=2x-1\)のグラフ上の、\(x=2\)の点なので
\(y\)座標は、\(y=2x-1\)に\(x=2\)を代入すると求められる
\(y=2 \times 2-1=3\)
\(a\)は点Aの\(y\)座標なので
\(a=3\)
例題2(一次関数の\(x\)軸の点)
次の図の、点Aを求めなさい。
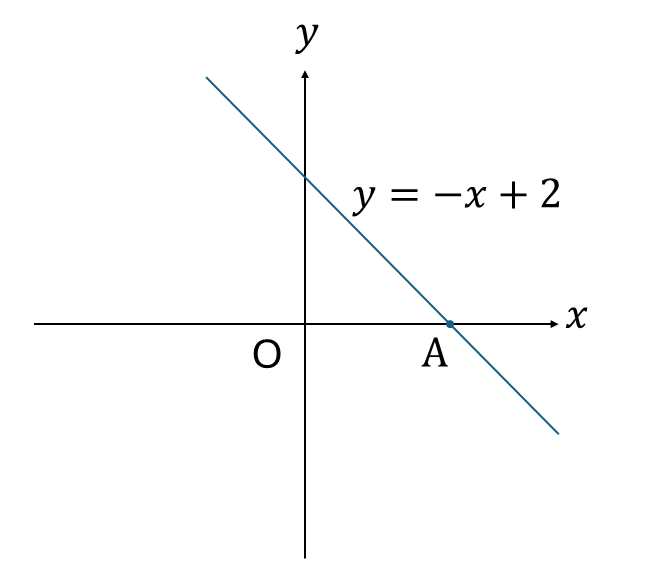
解説
点Aは\(x\)軸上の点だから、\(y\)座標は0
\(y=-x+2\)に\(y=0\)を代入すると
\(0=-x+2\)
\(x=2\)
よって求める座標は\(2,0\)
例題3(二次関数のグラフの点)
次の図の、\(a\)を求めなさい。
ただし、\(a<0\)とする。
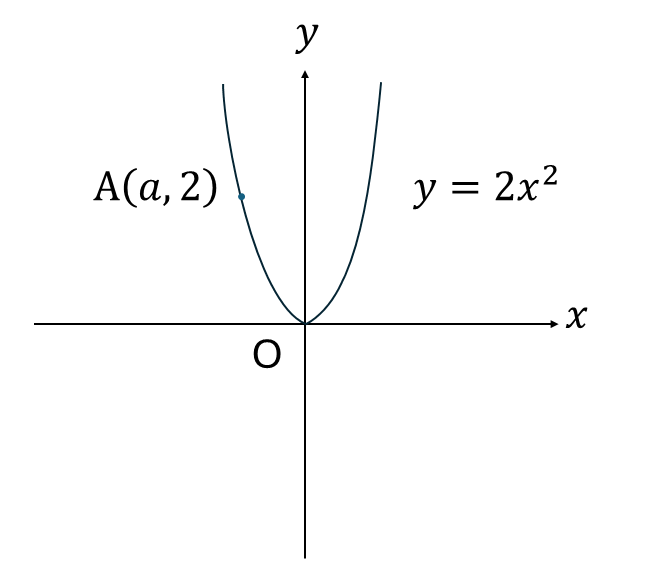
解説
点Aは、\(y=2x^2\)のグラフ上の、\(y=2\)の点なので
\(x\)座標は、\(y=2x^2\)に\(y=2\)を代入すると求められる
\(2=2x^2\)
\(x^2=1\)
\(x= \pm 1\)
\(a\)は点Aの\(x\)座標で、\(a<0\)なので
\(a=-1\)
例題4(一次関数どうしの交点)
次の図の、点Pを求めなさい。
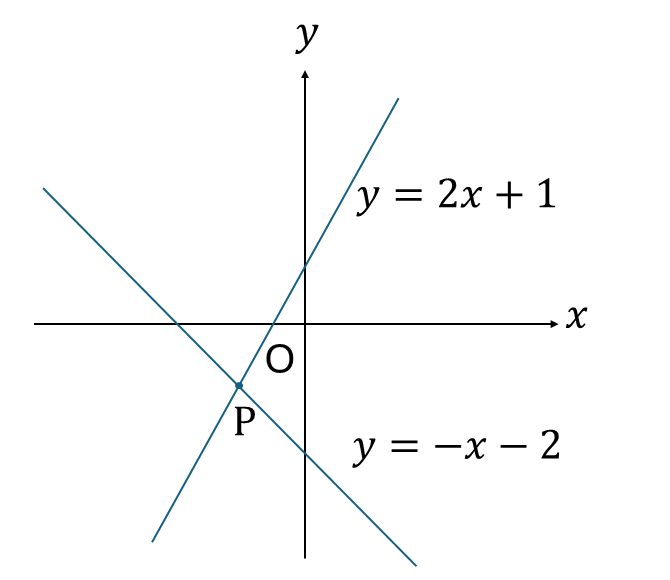
解説
\(y=2x+1\)と\(y=-x-2\)の交点
⇒\(y=2x+1\)と\(y=-x-2\)を連立
\(y=2x+1\)…①
\(y=-x-2\)…②
①を②に代入して
\(2x+1=-x-2\)
\(3x=-3\)
\(x=-1\)
①に\(x=-1\)を代入して
\(y=-1\)
よって点P(-1,-1)
例題5(一次関数と二次関数の交点)
次の図の、点P、Qを求めなさい。
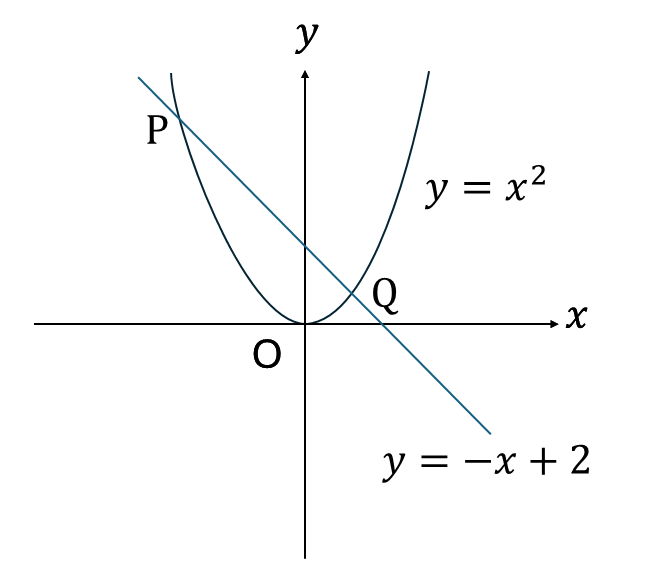
解説
\(y=x^2\)と\(y=-x+2\)の交点
⇒\(y=x^2\)と\(y=-x+2\)を連立
\(y=x^2\)…①
\(y=-x+2\)…②
①を②に代入して
\(x^2=-x+2\)
\(x^2+x-2=0\)
因数分解して
\((x+2)(x-1)=0\)
\(x=-2,1\)
それぞれ①に代入して
\(x=-2\)のとき\(y=4\)
\(x=1\)のとき\(y=1\)
よってP(-2, 4)、Q( 1, 1)
おわりに
点を求める問題は
- グラフ上の点で\(x\)、\(y\)のどちらかがわかっている
⇒グラフの式に代入 - 2つのグラフの交点
⇒グラフの式を連立
のどちらかです。
小問としての出題はもちろん、難しい問題を解くときにも必要になる操作です。
ここができるようになると、得点もアップしますし、関数の難しい問題の見え方も変わってきます。
がんばってください。




コメント