「一次関数のグラフの描き方がいまいちわからない」
そんなこと思っていませんか?
関数の単元以外ではあまり描く機会がないので、描き方があやふやな人も多いはず。
一次関数のグラフは3ステップでかんたんに描けます。
今回は、中2数学で習う一次関数のグラフで傾きが整数の場合について、描き方を整理してお伝えしたいと思います。

つまづく人が多い、分数が混じったグラフの描き方は、一次関数、グラフの描き方3ステップ(分数編)を参考にしてください。
直線のグラフの描き方
直線のグラフを描くときは、基本的に次の手順で行います。
- 直線を通る2点をとる
- 2点を通る直線を引く
中学2年生で習う直線のグラフには、次の3種類があります。
- 一次関数のグラフ
- \(x\)=〇のグラフ(\(x\)軸に垂直な直線)
- \(y\)=〇のグラフ(\(x\)軸に平行な直線)
どの直線も、基本的な描き方は同じです。
次は、この手順を特に一次関数に合わせて修正していきます。
一次関数の傾きと切片の基礎知識
一次関数のグラフを描くときに押さえておきたい基本です。
- グラフは直線
- 傾き:\(a\)
\(x\)が1増えると、\(y\)は\(a\)増える - 切片:\(b\)
グラフは、点\((0,b)\)を通る
一次関数のグラフの基本については、一次関数のグラフの形と見方の記事を参考にしてください。
一次関数のグラフ|傾きが整数のときの描き方の3ステップ
手順|一次関数のグラフの描き方3ステップ
一次関数のグラフを描くときは、次の3ステップで考えるとわかりやすいです。
- 切片をとる
- 傾きからグラフが通るもう1点を考える
- 2点を線で結ぶ
手順の解説
最初に説明した、直線の描き方の手順に沿って説明していきます。
直線を通る2点を考えるときに、最初に考えやすいのが切片の\(b\)です。
一次関数のグラフは必ず点\((0,b)\)を通ります。
まずは、この点をグラフ用紙にとってください。
もう1点は、傾きから考えます。
傾きが\(a\)ということは、\(x\)が1増加すると、\(y\)は\(a\)増加するということです。
だから、一次関数のグラフは、切片から横に1、縦に\(a\)進んだ点を通ります。

具体的には
- 傾き\(a\)が正
右に1、上に\(a\)の数だけ進んだ点 - 傾き\(a\)が負
右に1、下に\(a\)の数だけ進んだ点
をとります。
これで、直線を通る2点がわかります。
あとは、この2点を通る直線を引けば、一次関数のグラフを描けます。
まとめると、最初に説明した3つのステップになります。
次は、傾きが正と負、それぞれの場合の一次関数のグラフの描き方を例題で見ていきましょう。
一次関数のグラフの描き方を例題で見てみよう
例題1(一次関数のグラフの描き方:傾きが正の場合)
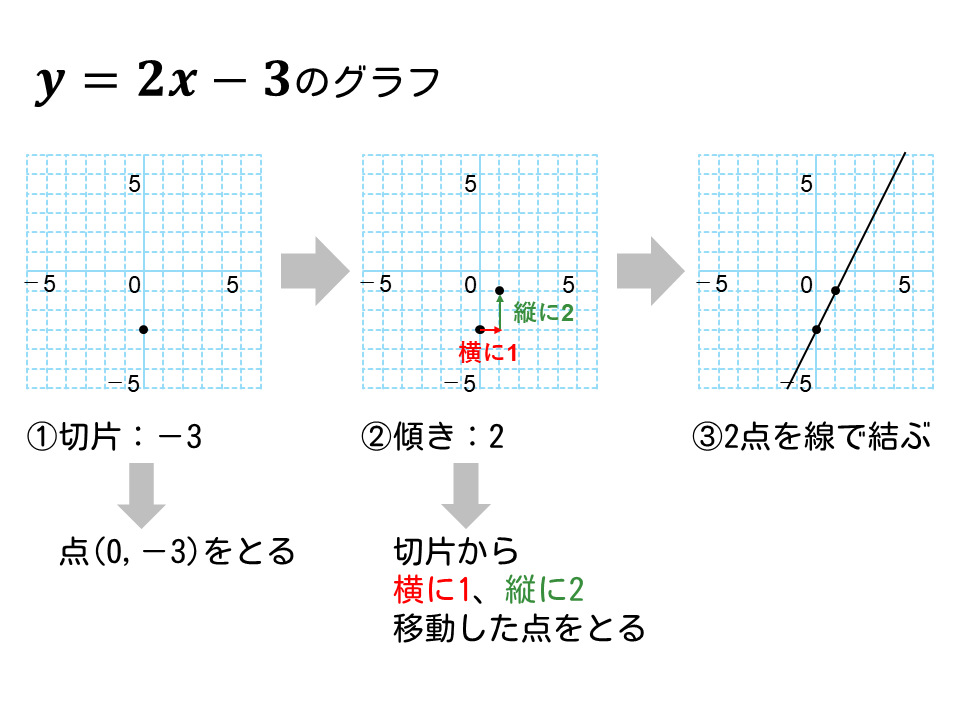
一次関数\(y=2x-3\)のグラフを描け。
解説
- このグラフの切片は-3
⇒点(0,-3)をとる - 傾きが2
⇒\(x\)が1増えると、\(y\)が2増える
⇒点(0,-3)から右に1、上に2進んだ点をとる - 2点を結ぶ直線を引く
この手順で描くと、下図のような一次関数のグラフが描けます。
例題2(一次関数のグラフの描き方:傾きが負の場合)
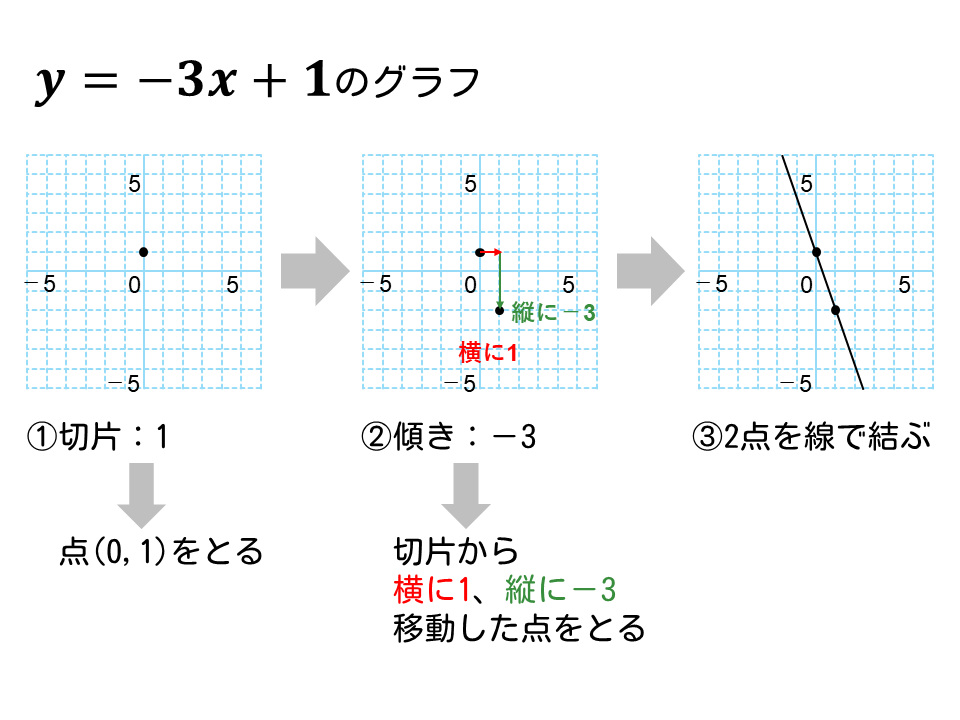
一次関数\(y=-3x+1\)のグラフを描け。
解説
- このグラフの切片は 1
⇒点(0, 1)をとる - 傾きが-3
⇒\(x\)が1増えると、\(y\)が3減る
⇒点(0, 1)から右に1、下に3進んだ点をとる - 2点を結ぶ直線を引く
この手順で描くと、下図のような一次関数のグラフが描けます。
この3ステップで描けない場合
この方法では、傾きや、切片が分数のときはこの描き方ができません。

「描けない」とは、テストでよく使われる「目盛り1の方眼用紙に描けない」という意味です。
整数の点でないと、点をとれないからです。
整数が傾きの一次関数のグラフは描けるけど、分数が傾きになると描けなくなる生徒は大勢見ました。
そのため、傾きや切片が分数である一次関数のグラフを描くためには、今回の記事で取り扱った3ステップを拡張していく必要があります。
一次関数のグラフの描き方の3ステップの拡張方法については、次の記事でご紹介します。

「最初から分数まで描ける方法を説明してくれてもいいのに」と思われるかもしれません。
ただ、最初は整数が傾きのグラフから始めた方が段階的に進めるので、定着しやすいんです。
おわりに
傾きが整数の一次関数のグラフは次の3ステップで描けます。
- 切片をとる
- 傾きからグラフが通るもう1点を考える
- 2点を線で結ぶ
これが描けるだけでも、一次関数の単元の定期テストではかなり得点が伸びると思います。
また、傾きや切片が分数である一次関数のグラフを描くときも、この描き方が基礎になります。
何度も手を動かして一次関数のグラフを描いて、描き方の手順を、意味からしっかり理解できるようにしていってください。





コメント