グラフは、点の集まりです。
何となくグラフを描ける人でも、実は「グラフの意味」をしっかり理解していないことがよくあります。
けれども、グラフの意味を正しく理解しておくと、
- なぜ関数の式に値を代入して点を求めるのか
- 交点をどのように求めるのか
といったことが納得できるようになります。
その結果、この単元の理解がより深まり、高校受験や高校数学でも使いやすい知識になります。
この記事では、一次関数のグラフを本格的に取り上げる前に、グラフの基礎である
について、図解を交えてわかりやすく解説します。
グラフの点の読み方、とり方
グラフ上の点は、「横の位置(\(x\))」と「縦の位置(\(y\))」で表します。
この2つをセットにしたものを 座標といいます。
たとえば、点Aが「原点から横に3、縦に2」のところにあるなら、その座標は A(3, 2) と書きます。
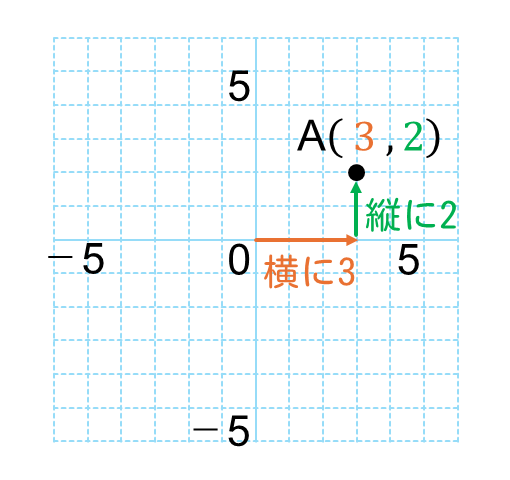
次の図の点Bのように、グラフ上の位置だけわかっている場合は、「原点から横、縦にどのぐらい動いているか」を軸から読み取ります。
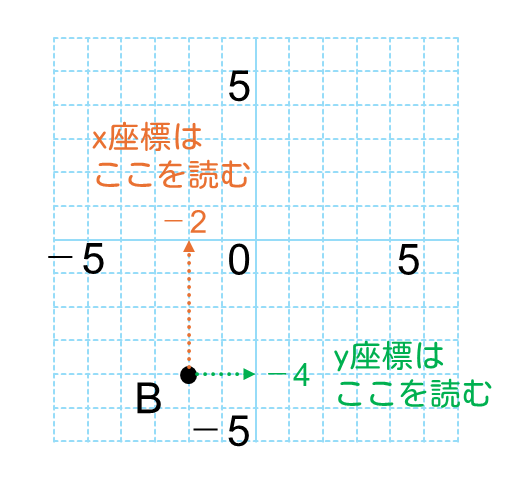
点Bの座標は B(-2,-4)と読み取れます。
もちろん、グラフ上の点も、これと同じように読みます。
関数のグラフとは?意味と考え方
見落としがちなグラフの意味
関数のグラフは、「関数の式を満たす点の集まり」です。
少し難しい言い方ですが、ここが理解できると関数の見方が大きく変わります。
それでは、具体例で見ていきましょう。
グラフの意味を具体例から見てみよう。
次の式について考えます。
\(y=2x+1\)
この式で、\(x\)の値をいくつか決めて\(y\)の値を求めると、次のような表が作れます。
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -5 | -3 | -1 | 1 | 3 | 5 |
次に、この表の\(x\)と\(y\)を、グラフ用紙にとります。
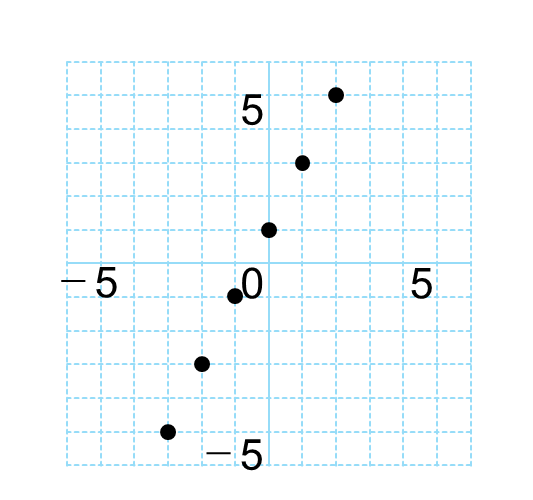
しかし、\(x\)の値は整数に限りません。
たとえば、\(x\)=0と\(x\)=1の間にも、無数の値が存在します。
また、この式では、\(x\)が1増えると\(y\)は2ずつ増えるという一定の割合で変化しています。
つまり、\(x\)の値を細かく変えていくと、無数の点をとることができます。
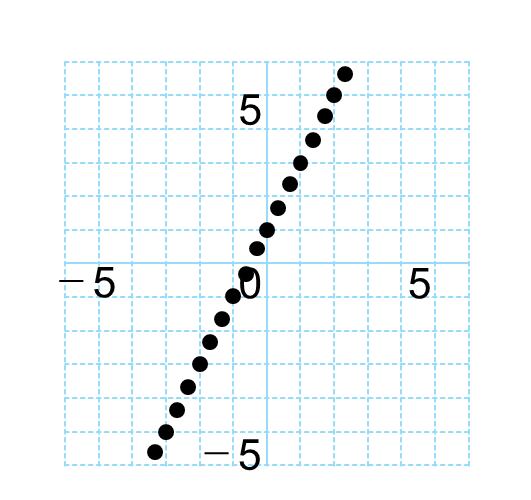
いちいち点を打つのは大変なので、それらの点を線で結んで表すのがグラフです。
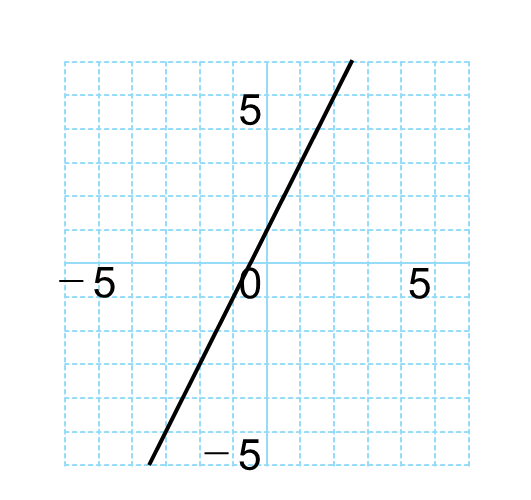
グラフとは、関数の式を満たす無数の点を線で表したもの
まとめると、関数の式を満たす\(x\)と\(y\)の組をいくつもとり、それらの点を線で結んだものがグラフです。
つまり、グラフは関数の式を満たす点の集まりということです。
グラフの読み方
グラフが描いてあると、次のことが計算しなくてもわかります。
- ある\(x\)に対応する\(y\)の値
- ある\(y\)に対応する\(x\)の値
これも具体例で見てみましょう。
下の図は、\(y=-2x+1\)のグラフです。
このグラフから、値を読み取る手順をご説明します。
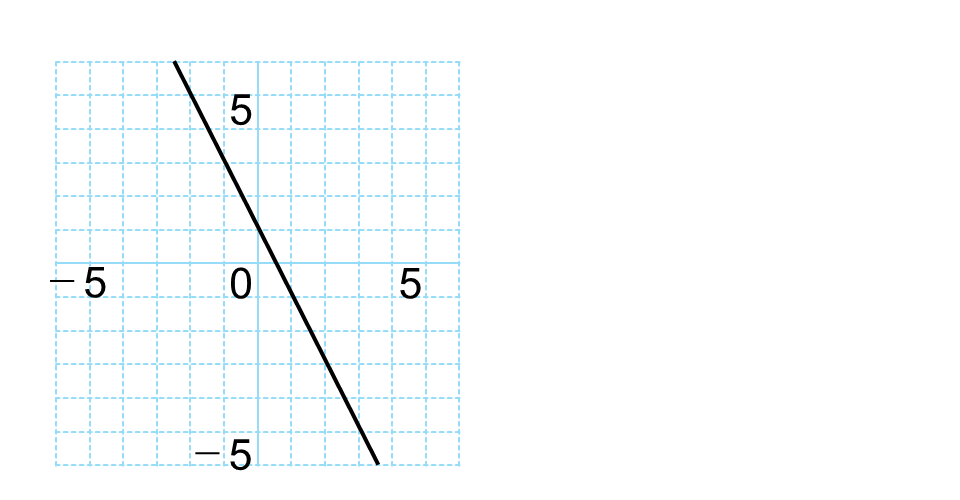
\(x\)から\(y\)を読む
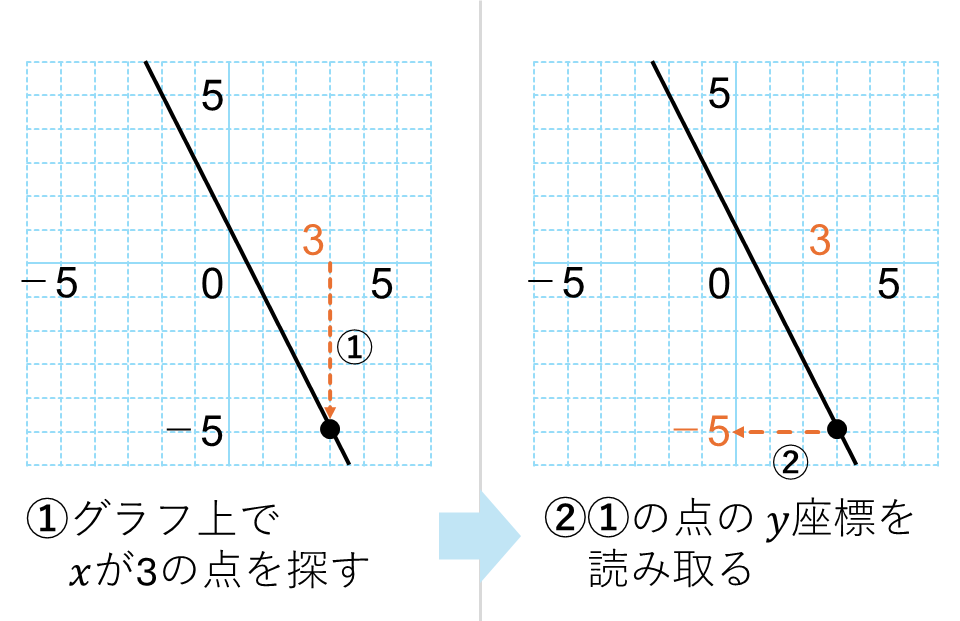
\(x\)=3のときの\(y\)の値をグラフから読み取る手順は、次の通りです。
- グラフ上で、\(x\)=3の点を探す
- ①で探した点の\(y\)座標を読み取る
- \(y=-5\)とわかる
関数の式
\(y=-2x+1\)
に\(x=3\)を代入すると
\(y=-2 \times 3 +1 = -5\)
となり、確かにグラフからの読み取り結果と一致しています。
大事なことなので、何度も繰り返しますが、グラフは関数の式を満たす点の集まりです。
だから、グラフ上のどの点の\(x\)座標と\(y\)座標の組も、必ずグラフの式を満たします。
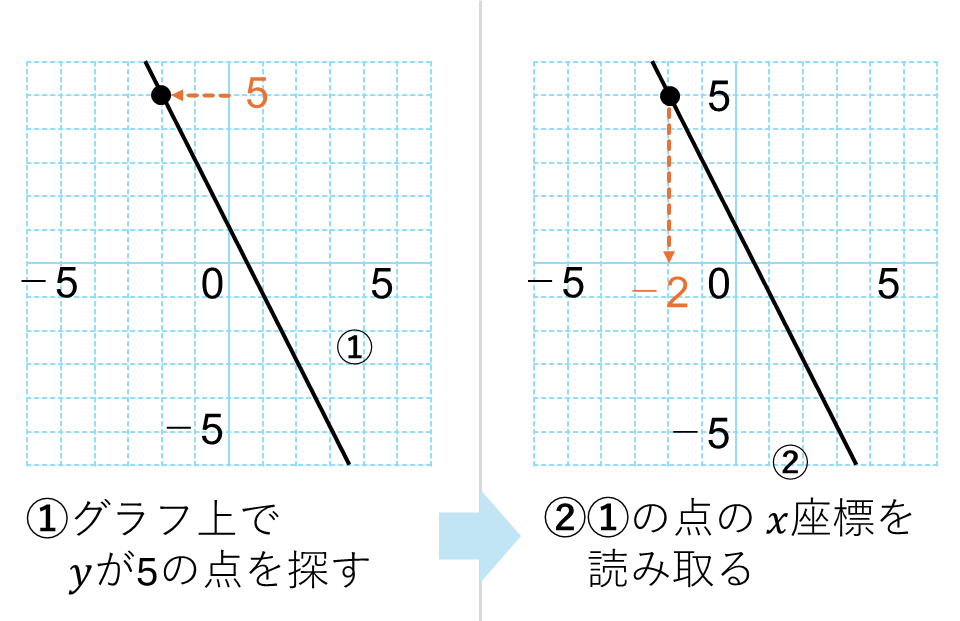
\(y\)から\(x\)を読む
\(y\)=4のときの\(x\)の値をグラフから読み取ると、次のようになります。
- グラフ上で、\(y\)=4の点を探す
- ①で探した点の\(x\)座標を読み取る
- \(x=-2\)とわかる
関数のグラフ:x座標からy座標を読み取る
以上の通り、グラフから
- \(x\)に対応する\(y\)
- \(y\)に対応する\(x\)
を読み取ることができることがわかります。
おわりに
今回の内容は、以下の通りです。
正直、今の範囲では、グラフの必要性をあまり感じないと思います。
しかし、関数が難しくなるほど、グラフが必要になってきます。
今の時期は、後の勉強のための準備期間と思ってがんばってください。





コメント