「切片が分数のときってどうやってグラフを描けばいいの?」
そんな経験ありませんか?
定期テストで出題される「一次関数のグラフを描く問題」は、目盛り間隔が1のことがほとんどです。
だから、切片が分数だと、切片がとれなくなってしまい描き方がわからなくなってしまいます。
この記事では、苦手にする人が多い「切片が分数である一次関数のグラフの描き方」を、具体的な手順と例題を使ってわかりやすく解説します。
【関連記事】
- 基本的なグラフの描き方に自信がない方は先にこちらをお読みください
「切片⇒傾き」で考えるグラフの基本的な描き方についてまとめました。
定期テストでの出題のほとんどはこちらの方法で描けます。
また、入試で道具としてグラフを使う場合も、こちらの描き方だけわかっていればOKです。
👉「切片⇒傾き」で考える!一次関数のグラフ、基本の描き方
分数が切片のグラフが描きづらい理由
定期テストでは、基本的に目盛りが1のグラフ用紙を使います。
そのため、切片が分数だと、グラフを描く最初に切片をとるときに、切片が目盛りの間にきてしまいます。
そのため、「切片をとって、傾きからもう1点を考えて」といういつもの考え方が使えなくなってしまうのです。
そこで、分数が切片のグラフを描く問題では、切片をとらずにグラフを描く必要があるのです。

考えをまとめるための図としてグラフを描く場合は、特に気にしなくても大丈夫です。
「定期テストのグラフを描く問題」のときに描けないというだけです。
切片が分数である一次関数のグラフの描き方
切片が分数である一次関数のグラフを描く手順
解説
切片が分数のグラフで問題になるのは、「最初に切片がとれない」ということです。
そのため、切片とは別に、\(x、y\)が整数の点をとれないか探します。
これは、適当な\(x\)の値を式に代入して、\(y\)を計算してみるしかありません。
そんなに大きな数字になることはないので、\(x=1,-1,2,-2…\)のように小さい整数から順に代入すると見つけやすいです。
たとえば、
\(\displaystyle y= \frac{2}{3}x+\frac{1}{3}\)
のような式であれば、
\(x=1\)のとき
\(\displaystyle y=\frac{2}{3} \times 1 + \frac{1}{3}=1\)
なので、点( 1, 1)を通るとわかります。
あとは、切片が整数のときと同じように考えれば大丈夫です。
傾きが\(\displaystyle \frac{1}{3}\)なので、点( 1, 1 )から右に 3、上に 1 の点をとれば、下図のようなグラフを描くことができます。

一次関数のグラフの描き方で一番ネックになるのが、この傾きの使い方です。
ここがわかればグラフは簡単に描けるようになります。
別記事でさらに詳しく解説しているので、イメージがしづらければこちらをお読みください。
👉具体例でわかる!グラフ上での傾きの考え方!
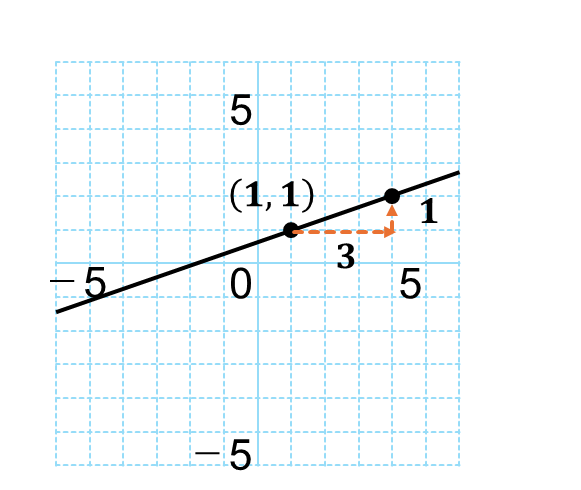
例題で分数が切片の一次関数のグラフを考えてみよう
例題
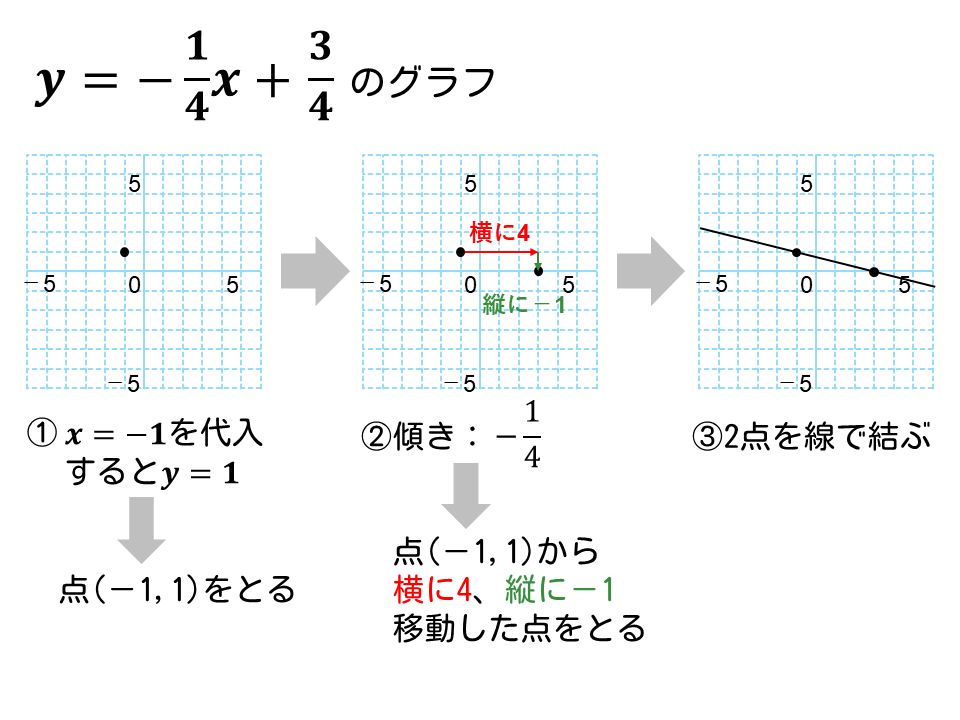
\(\displaystyle y= -\frac{1}{4}x+\frac{3}{4}\)
【解説】
- \(x=-1\)のとき、\(y=1\)
よって、点(-1, 1)を通るとわかります
点(-1, 1)をとります - (傾きの分母)= 4
(傾きの分子)= -1
点(-1, 1)から、横に 4、下に-1、進んだ点をとります - 2点を結ぶ直線を引きます
解答は下図参照。
おわりに
この記事では、切片が分数である一次関数のグラフの描き方について説明しました。
切片が分数のグラフは、最初の点のとり方が少し違うだけ。
それ以外は、整数のときとまったく同じです。
また、この描き方は「定期テストでグラフを描く問題」のときだけ必要になるということも知っておいてください。
自分の考えをまとめるためだけなら「切片をとる→傾きからもう1点をとる」で十分なのです。
自分の手でグラフを描けるようになると、必ず自信につながります。
あせらず、しっかり整理して練習していきましょう。
【関連記事】
- 次の解説記事を読む方はこちら
直線の式のほとんどは一次関数ですが、例外が2つあります。
それが\(「x=a」,「y=b」\)のグラフです。
このグラフの意味や、グラフの描き方、直線のグラフの考え方などについて解説します。
👉一次関数ではない直線「x=a」「y=b」をていねいに解説 - この範囲の演習記事を読みたい方はこちら
整数・分数どちらのタイプもふくめて、一次関数のグラフを実際に描いて練習できる演習記事です。
👉一次関数のグラフ:描き方の演習 - グラフの読み取り方の記事に進む方はこちら
グラフから式を読み取るときも「切片⇒傾き」で考えます。
グラフの描き方と、グラフから式の読み取り方の2つができれば、「式⇔グラフ」のイメージは完璧になります。
ぜひ、しっかり整理してグラフを自由に使えるようにしてください。
👉「切片⇒傾き」の順で考える!一次関数、グラフから式の読み取り - 基本的なグラフの描き方を再確認したい方はこちら
「切片⇒傾き」で考えるグラフの基本的な描き方についてまとめました。
分数が切片のときの描き方と併せて整理しておくと、定期テストのグラフを描く問題は完璧になります。
👉「切片⇒傾き」で考える!一次関数のグラフ、基本の描き方 - 一次関数のまとめに戻る方はこちら
関数は、抽象的で取り組みづらい反面、同じ操作が繰り返し出てくるので、コツが掴めると得意にしやすい分野でもあります。
考え方からていねいに解説しているので、ぜひ先々まで活用できるかたちで知識を身に付けてください。
👉【完全攻略】一次関数の解き方・考え方を基礎からじっくり


コメント