「変域の求め方って、結局どう考えればいいの?」
そんな疑問をもったことはありませんか?
中2の一次関数から始まり、中3の二次関数、高校数学まで、関数を学習するかぎり“変域”は必ず登場します。
でも実は、変域の求め方はどの関数でも 同じ考え方 で進められます。
そのカギが、
「まずグラフ全体を考えて、そこから有効な部分だけを絞り込む」
という手順です。
この記事では、一次関数を例にしながら、どの関数にも通用する変域の考え方をわかりやすく解説します。
【前回の記事を読みたい方はこちら】
\(y\)の変域ってどうやって考えたらいいの?
\(y\)の変域は、グラフの有効な部分だけを描いて考える
変域を求める問題は、「\(x\)の変域が与えられる⇒\(y\)の変域を求める」という形式で出題されます。
この問題は、有効な範囲のグラフを描き、そのグラフの最も低い\(y\)座標と最も高い\(y\)座標を読み取るのが基本的な解法の流れです。
そして、次の4ステップで考えると、有効な部分が整理しやすくなります。
変域の求め方を詳しく解説
変域って何?
簡単に言うと、文字がとる値の範囲のことです。
つまり、「この文字(\(x,y\))はこの範囲で考えてくださいね」という決めごとです。
たとえば、
\(x\) の変域が「\(1 ≦x≦ 5\)」
⇒「\(x\) は1 から 5までの間の値で考えます」
という意味です。
グラフ上での変域の意味
グラフは、関数の式を満たす\(x,y\)の集まりです。
だから、\(x\)の変域が決められていると、グラフも変域内だけが有効ということになります。
そのため、有効な部分のグラフを描くことができれば、\(x,y\)の範囲が一目でわかるようになります。
有効な範囲のグラフの描き方
いきなり有効な範囲のグラフを考えることもできないわけではないですが、
それだと少し考えにくいです。
そのため、次の手順でグラフを描いてください。
- 変域がないものとして関数のグラフを点線で描く
- \(x\)の変域を座標内に書く
- グラフの変域内にある部分を実線でなぞる
このように描くと、グラフの定義域内の部分だけを、実線として描くことができます。
変域の考え方を例題で見てみよう
例題
\(y=2x+1\)の\(-1≦x≦2\)の範囲における\(y\)の変域を答えなさい。
【解説】
まず、\(y=2x+1\)のグラフを点線で描きます。
切片1、傾き2のグラフなので、切片と切片から右に1上に2の点をとるとグラフが描くことができます。
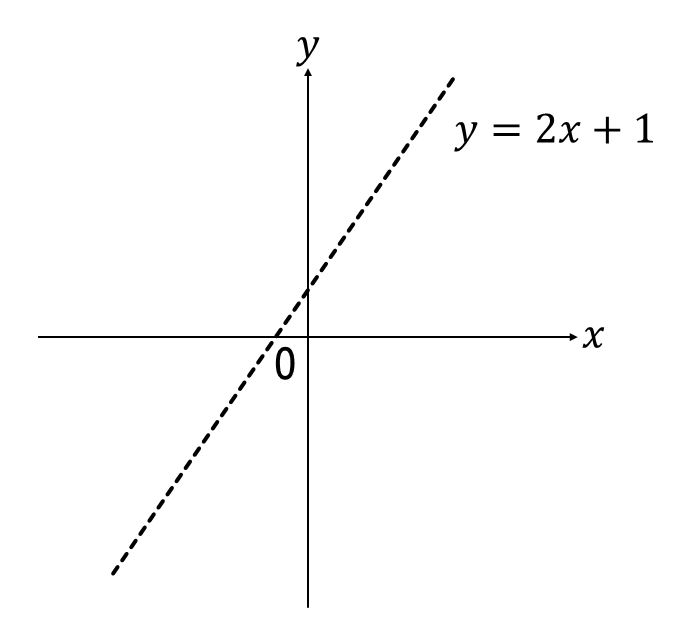
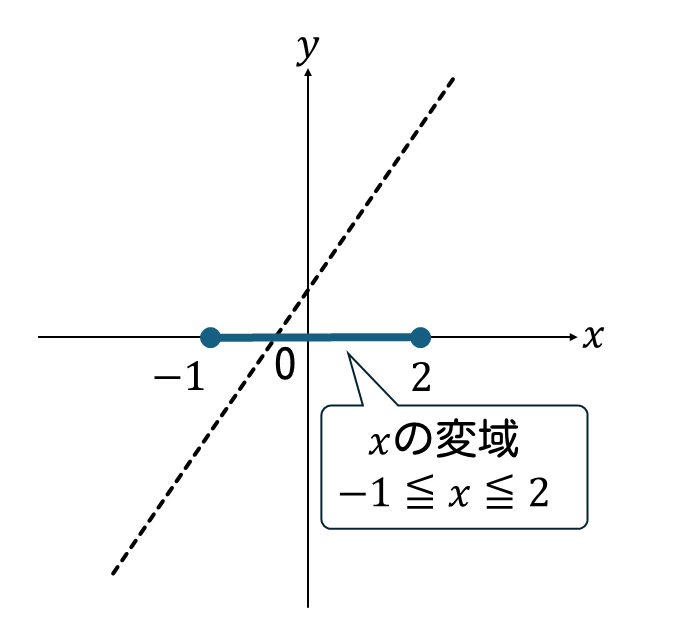
次に、\(x\)の変域\(-1≦x≦2\)を\(x\)軸上に書き込みます。
それができたら、グラフの\(x\)の変域内にある部分だけを実線でなぞります。
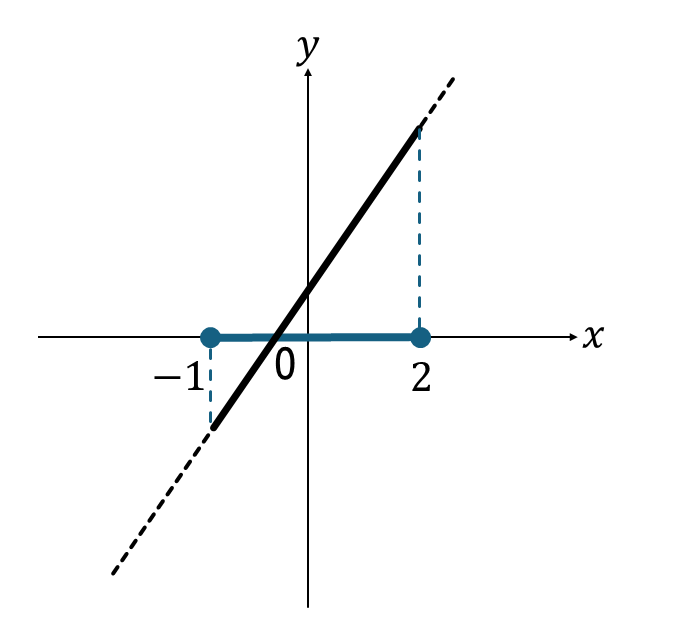
最後に、\(x=-1\)と\(x=2\)のときの\(y\)座標を、関数の式から計算し、
グラフの実線部の\(y\)座標の下端(最小値)から上端(最大値)までを読み取ります。
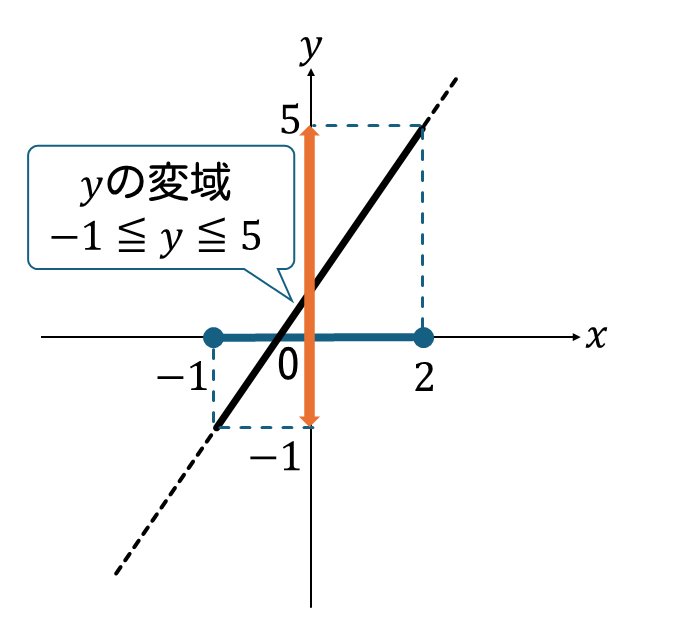
すると、グラフから\(-1≦y≦5\)とわかります。
有効な範囲のグラフを描くときの思考メソッド
数学では、詳細な条件からではなく、「まず全体を考える⇒詳細条件で絞り込む」という考え方をはよく使います。
今回の変域の考え方であれば、
「まず関数のグラフとして必要な全体像を考える⇒ \(x\)の変域の条件を満たす部分(有効な範囲)だけを実線で絞り込む」
という手順を踏みます。
おわりに
今回は、変域の考え方について解説しました。
変域を求める手順は、どの関数(中3の二次関数、高校の関数など)でも共通しており、以下の3ステップで考えます。
- 関数全体のグラフを描く
- 変域でグラフの有効な範囲を出す
- \(y\)の範囲を読み取る
この問題に取り組むことは、「座標の読み方」や「グラフの意味・描き方」、「グラフ上の点の求め方」など、複合的な力のレベルアップにつながります。
最初は難しく感じるかもしれませんが、変域をきちんと求められるようになれば、どんな関数を前にしても考え方で迷うことはなくなります。
がんばってください。


コメント