中学生～高校生に向けてのやさしい関数ナビ、週1ぐらいで更新中

【定期テスト対策・中2数学】一次関数ではない直線「x＝a」「y＝b」をていねいに解説

中2の関数（一次関数）
2025.10.19

「\(x\)軸に平行な直線が\(y\)=〇で、\(x\)軸に垂直な直線が…」
そんなふうに迷った経験はありませんか？

一次関数以外でも、グラフが直線になる式に「\(x\)=〇」「\(y\)=〇」があります。

とても重要な内容なので、意味をきちんと理解しておく必要がありますが、塾で教えていたころは、単純に暗記で済ませようとする人も多かったです。
ただ、ここは言葉の暗記だけで済ませてしまうと、2つを混同してしまってすぐにわからなくなってしまいます。
そのため、式・グラフの意味からしっかり理解しておく必要があります。

この記事では、一次関数以外の直線の式である「\(x\)=〇」「\(y\)=〇」についてわかりやすく解説します。

この記事でわかること

一次関数以外の直線の式である「\(x\)=〇」「\(y\)=〇」について、次のことがわかります。

  • 式のグラフ上での意味
  • \(x\)軸、\(y\)軸との関係性
  • グラフの描き方

【前回の記事を読む方はこちら】

グラフ用紙内での\(x=a\)、\(y=b\)ってどういう意味？

\(x=a\)、\(y=b\)のグラフとしての考え方

\(x=a\)、\(y=b\)のグラフは、それぞれ次のように考えます。

  • \(x=a\)
    ⇒常に\(x\) の座標が\(a\)
    ⇒\(y\)軸と平行、\(x\)軸に垂直な直線
  • \(y=b\)
    ⇒常に\(y\) の座標が\(b\)
    ⇒\(x\)軸と平行、\(x\)軸に垂直な直線

\(x=a\)、\(y=b\)のグラフとしての考え方を詳しく解説

\(x=a\)や\(y=b\)と聞くと、おそらく\(x\)や\(y\)の1つの値のことを言っていると考えてしまう人がほとんどじゃないでしょうか？

もちろんそれも間違いではありません。
ただ、これを関数として見た場合、
つまり「\(x\)の値に対して\(y\)がどう変わっているか」
と考えると見方が変わります。

\(x=a\)のグラフの考え方を具体例で

たとえば、\(x=2\)という式があったとき、
\(y\)の値は何も書かれておらず、\(x\)が2ということなので、

\(\displaystyle (x,y)=(2,-1),(2,1),(2,3),…\)

のように、\(x=2\)であれば、
\(y\)はいくつでも大丈夫ということになります。

\(x\)座標は、\(y\)軸からどれぐらい離れているかを表すので、
グラフにすると下図のように、\(y\)軸と平行、\(x\)軸に垂直な直線になります。

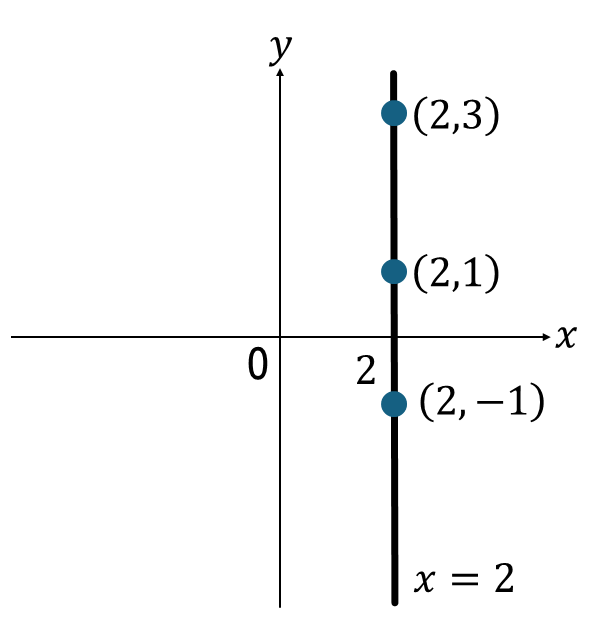
\(y=b\)のグラフの考え方を具体例で

同じように、\(y=3\)という式ならば、

\(\displaystyle (x,y)=(-1,3),(1,3),(3,3),…\)

のように、\(y=3\)であれば、
\(y\)はいくつでも大丈夫ということになります。

\(y\)座標は、\(x\)軸からどれぐらい離れているかを表すので
グラフにすると下図のように、\(x\)軸と平行、\(y\)軸に垂直な直線になります。

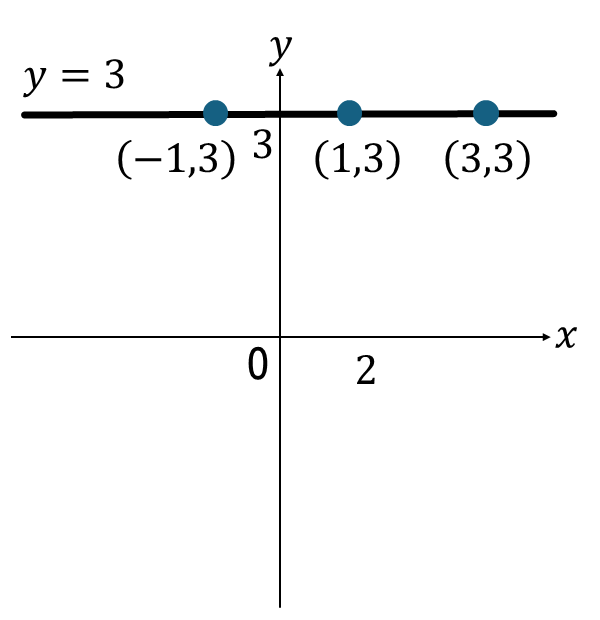
大事なことなので何度でも繰り返しますが、「グラフは式を満たす点のあつまり」です。
「\(x=2\)」は「\(x=2\)を満たす点のあつまり」
「\(y=3\)」は「\(y=3\)を満たす点のあつまり」
と見ることができれば、グラフの形もしっくりくると思います。
もし、「グラフは式を満たす点のあつまり」という意味がイメージしづらければこちらの記事をお読みください。
👉「グラフは式を満たす点のあつまり」の意味を比例のグラフでやさしく解説

\(x=a\)、\(y=b\)のグラフはどうやって描いたらいい？

\(x=a\)、\(y=b\)のグラフの描き方

グラフは、次の手順で描くことができます。

  1. 通る2点を適当に決める
  2. 2点を通る直線を引く

\(x=a\)、\(y=b\)のグラフの描き方を詳しく解説

直線は、通る2点がわかれば、必ず一本に決まります。
そのため、式を満たす点を2つ決めてください。

たとえば、\(x=2\)のグラフを描くときであれば、
\(y\)の値はいくつでもいいので、
\((x,y)=(2,1),(2,2)\)
のように、考えやすい数字を適当に決めてしまってください。

あとは、この2点を線で結べば、グラフを描くことができます。

例題1（\(x=a\)のグラフ）

\(x=3\)のグラフを描いてください。

【解説】

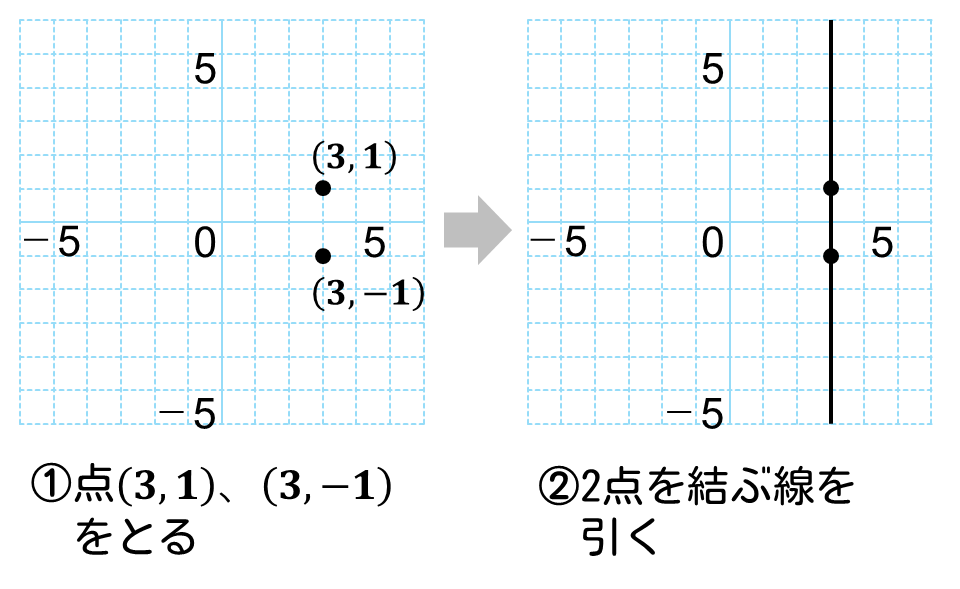
  1. \(x\)座標が3である点、(3 , 1)、(3,－1)をとる
  2. 2点を通る直線を引く
x=aのグラフ

例題2（\(y=b\)のグラフ）

\(y=-1\)のグラフを描いてください。

【解説】

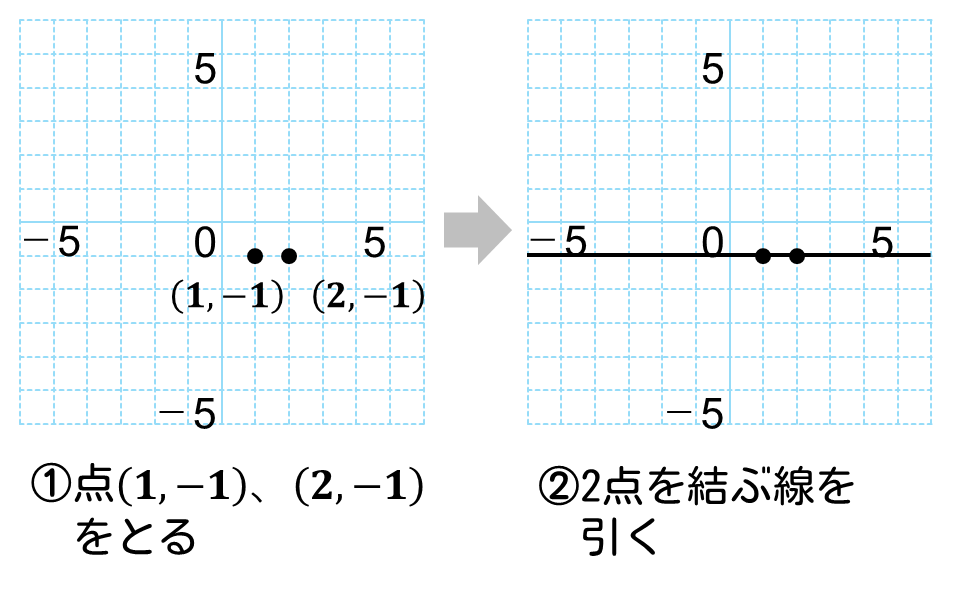
  1. \(y\)座標が－1である点、(1 ,－1)、(2,－1)をとる
  2. 2点を通る直線を引く
y=bのグラフ

直線のグラフを描くときの思考ロジック

このグラフに限った話ではないですが、直線の式は通る2点がわかれば必ず引けます。
そのため、「直線」という言葉が出たら、「2点はわかるのか？」という思考が出るようにしておくと、とっさにわからなくなっても、困らずに済みます。

与えられた条件から考えるのは考えやすいですが、何もないところに自分から数字を足すという発想は実は結構難しいです。

だから、「直線⇒2点」という考えの型はすごく大事になります。

おわりに

今回は、一次関数ではない直線の式「\(x=a\) と\(y=b\)」のグラフについて解説しました。

この2つの式が「単なる値」ではなく、「座標平面上の点の集まり（直線）」として理解できるようになれば、座標を見る力が格段に向上した証拠です。

慣れないうちは「\(x=a\)は\(x\)の値が\(a\)1つだけ」という感覚が抜けにくいかもしれませんが、焦らず1つずつグラフを描き、「どの\(y\)の値に対しても\(x\)が\(a\)になっている」という感覚をつかんでいきましょう。

頭の中のモヤモヤがきっと晴れます。
応援しています！

← 一つ前のページに戻る

【関連記事】

コメント