一次関数は、中2数学で非常に重要な単元です。
式からグラフを描く方法や、グラフから式を読み取る方法を理解すると、テストだけでなく応用問題にも対応できます。
この記事では、切片や傾きの意味をふり返りながら、整数・分数どちらの傾きにも対応できるように、グラフの描き方・読み取り方を例題付きでわかりやすく解説します。
関連記事
【前回の解説記事を読みたい方はこちら】
- 一次関数のグラフで、傾き、切片がグラフ上でどういう動きをするかについてまとめました。
👉一次関数のグラフとは？傾き・切片の意味をわかりやすく解説
【演習問題を中心に進めたい方はこちら】
- 整数・分数どちらのタイプもふくめて、一次関数のグラフを実際に描いて練習できる演習記事です。
一次関数のグラフ：描き方の演習
一次関数のグラフを考えるための前提となる知識
一次関数の「式⇔グラフ」を考えるときに押さえておきたいポイントは次の3つです。
この特徴を使って、これから関数の式⇔グラフの関係を見ていきます。
しっかりおさえておきましょう。
グラフ上での変化と傾きの関係は、グラフを描いたり、関数の式を読み取ったりする上でとても重要です。
次の記事でまとめたので、理解を深めたいときは次の記事を読んでください。
👉一次関数の傾きをグラフで考えよう
「どうして一次関数のグラフは直線になるの？」、「傾き、切片って何？」という方は、こちらをお読みください。
👉一次関数のグラフとは？傾き・切片の意味をわかりやすく解説
一次関数のグラフの描き方（関数の式⇒グラフ）
一次関数のグラフを描く手順
解説
一次関数の式は直線です。
直線のグラフは、通る2点をとって直線で結ぶと引くことができます。
まず、いちばん考えやすい点は切片です。
ここを最初にとります。
次に、切片から右に移動した、\(x\)座標、\(y\)座標が整数の点を、傾きを使って考えます。
グラフ上での変化と傾きの関係は、
\( \displaystyle a = \frac{\text{上下の移動}}{\text{右への移動}}\)
と表せます。
たとえば、
- 傾き\(a=2\)
切片から右に1、上に2移動した点 - 傾き\(\displaystyle a = -\frac{3}{2}\)
切片から右に2、下に3移動した点
のように考えることができます。
これを使って2点目をとります。
2点目がとれたら、あとは2点を通る直線を引けば、関数のグラフが描けます。
例題で一次関数のグラフの描き方を見てみよう
例題1（一次関数のグラフの描き方：傾きが正の場合）
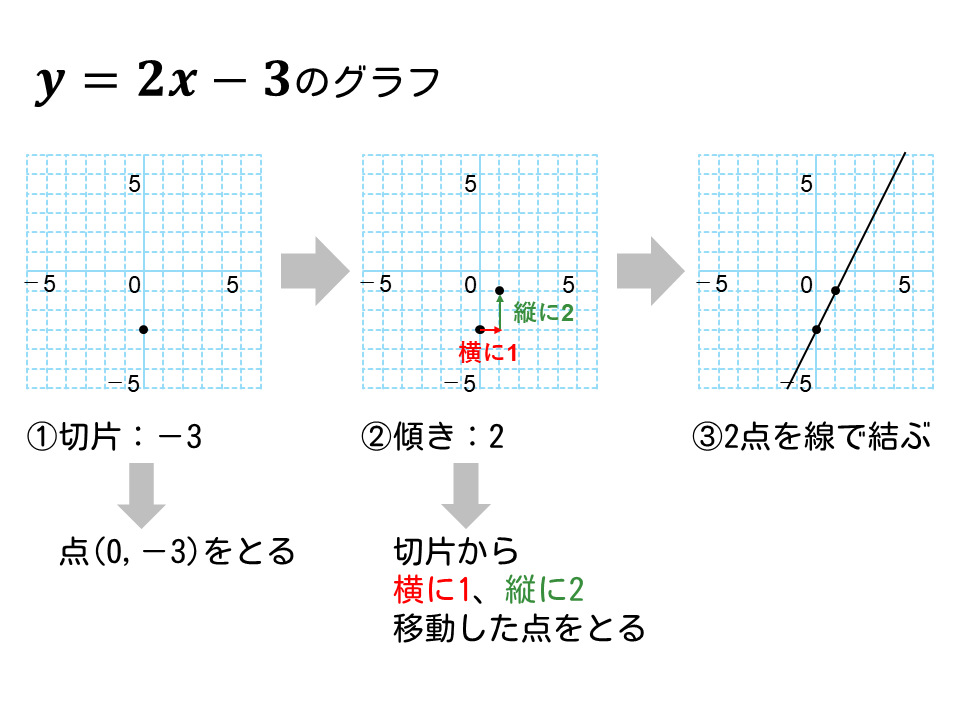
一次関数\(y=2x-3\)のグラフを描きなさい。
解説
- このグラフの切片は－3
点(0,－3)をとる - 傾きが\(\displaystyle 2= \frac{2}{1}\)
（傾きの分母）= 1
（傾きの分子）= 2
切片から右に1、上に2進んだ点をとる - 2点を結ぶ直線を引く
この手順で描くと、下図のような一次関数のグラフが描けます。
例題2
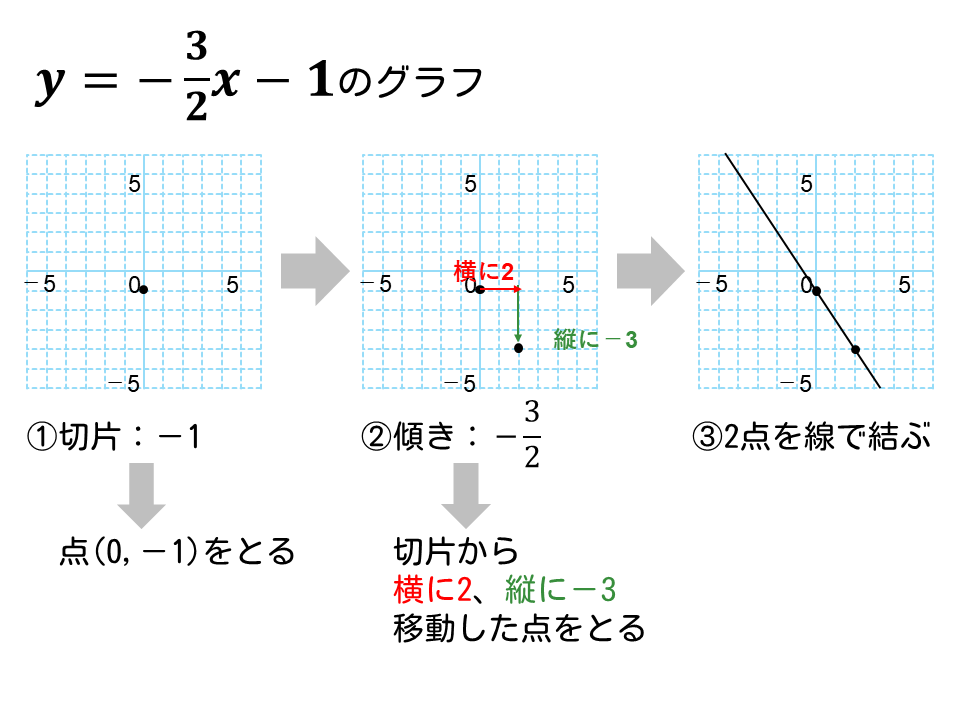
\(\displaystyle y= -\frac{3}{2}x-1\)のグラフを描きなさい。
解説
- このグラフの切片は 1
点(0, 1)をとる - 係数の前にマイナスがついているので、分子が負の数と考える
（傾きの分母）= 2
（傾きの分子）= －3
切片から、右に 2、下に 3、進んだ点をとる - 2点を結ぶ直線を引く
この手順で描くと、下図のような一次関数のグラフが描けます。
定期テストに限った話ですが、この方法でグラフが描けない場合があります。
それは、切片が分数のグラフです。
描けない理由と描き方を別記事でまとめましたので、次の記事をお読みください。
一次関数のグラフから関数の式の読み取り（グラフ⇒関数の式）
手順のコツ
解説
まず、わかりやすいところから見ていきます。
\(y\)軸を通る高さ（切片\(b\)）はすぐにわかるので、ここを最初に読み取ります。
次に、切片から右に動いて\(x\)座標、\(y\)座標が整数の点を見つけます。
切片からその点まで、右にいくつ動いたか、上下にいくつ動いたかを読み取ります。
読み取りできたら、次の式で傾きを計算できます。
\(\displaystyle \text{傾き} a = \frac{\text{上下の移動量}}{\text{右への移動量}}\)
これで、\(a\)、\(b\)の値がわかるので、\(y=ax+b\)の式に当てはめれば関数の式がわかります。
例題で一次関数の式の読み取り方を見てみよう
例題3（傾きが整数）
次のグラフの関数の式を求めなさい。
解説
- 切片を読み取る
⇒切片は－1 - 切片から右に移動して、\(x\)座標、\(y\)座標が整数の点を見つける
- 右への移動量、上下の移動量を読み取る
⇒右へ 1、下に 3 - \(\displaystyle \text{傾き}=\frac{\text{上下の移動量}}{\text{右への移動量}}\)
から、傾きを計算する
\(\displaystyle \text{傾き}=\frac{-3}{1}=-3\)
よって関数の式は
\(y=-3x-1\)
例題4（傾きが分数）
次のグラフの関数の式を求めなさい。
解説
- 切片を読み取る
⇒切片は－2 - 切片から右に移動して、\(x\)座標、\(y\)座標が整数の点を見つける
- 右への移動量、上下の移動量を読み取る
⇒右へ 4、上に 1 - \(\displaystyle \text{傾き}=\frac{\text{上下の移動量}}{\text{右への移動量}}\)
から、傾きを計算する
\(\displaystyle \text{傾き}=\frac{1}{4}\)
よって関数の式は
\(\displaystyle y=\frac{1}{4}x-2\)
おわりに
この記事では、一次関数の「式⇔グラフ」の関係を学びました。
まず切片をとり、傾きを使ってもう1点を考えると、簡単にグラフを描けます。
また、グラフから切片と傾きを読み取れば、関数の式もわかります。
これらの基本を押さえておくと、応用問題にもスムーズに取り組めます。
一次関数の式とグラフの関係が見えるようになると、一次関数の見え方もぐっと変わります。
慣れるまでは大変だと思いますが、演習を重ねると、だんだんできるようになってきます。
がんばってください。
関連記事
【次の解説記事を読みたい方はこちら】
- 切片が分数のときの一次関数のグラフの描き方についてまとめました。
👉切片が分数である一次関数のグラフの描き方
【この範囲の演習記事を読みたい方はこちら】
- 整数・分数どちらのタイプもふくめて、一次関数のグラフを実際に描いて練習できる演習記事です。
一次関数のグラフ：描き方の演習
【一次関数の学習目標を確認したい方はこちら】
- 定期テスト向けに一次関数の学習目標についてまとめました。
👉一次関数：変化の割合、レベル別演習
コメント